スカラー、配列
スカラー、配列(1次元配列、2次元配列、・・・)の関係を図示すると下図のようになります。
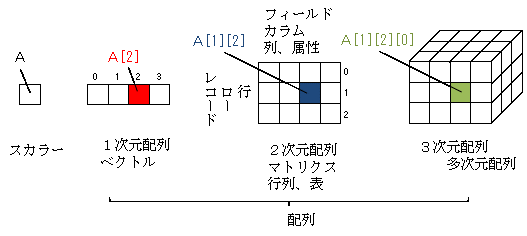
- 配列とは通常は同じ型(整数型、浮動小数点型、文字列)の集合です。アプリケーションによっては、異なる型が混在することもあります。
- 配列には、1次元配列、2次元配列、3次元配列、… があり3次元以上の配列を多次元配列といいます。
また、1次元配列、2次元配列には図に掲げたような別名があります。 - 配列のうち、一般によく用いられているのは1次元配列と2次元配列です。2次元配列は、数値解析の分野では行列と呼ばれ、行列の計算は大きな分野になっています。また、ビジネス分野では関係データベース(RDB)が広く用いられていますが、その表は2次元配列です。
- 配列の中の一つ(上図の色の部分)を要素といいます。
- プログラムの中で配列の要素を指定するには、A[2], A[1][2] のように、先頭からの番号で指定します(Aは配列変数名)。その番号は、現在広く用いられている言語(Java, Javascript, Cなど)では0から始まりますが、1から始まる言語(COBOL, Rなど)もあります。
- A[i][j] の i. j のような要素変数を添字といいます。A[i][j] の [] の順序は、通常の2次元配列では、[行(縦)方向]、[列(横)方向]の順になります。
行列
ここでは、数値解析分野での2次元配列、すなわち、行列に関する基本的事項を対象にします(関係データベースとしての2次元配列に関しては、正規化とRDBで扱っています)。
- 行列のサイズ
- 行列の縦・横の大きさのことです。上図はは縦は3行で横は4列ですので、Aのサイズを 3×4 といいます。
なお、行数をM、列数をNで表すのが慣例で M×N で表します。
特殊な行列
- 正方行列
- M=Nの行列です、
1 2 3
4 5 6
7 8 9 - 対角行列
- 対角線以外の要素が0である正方行列です。
1 0 0
0 5 0
0 0 9 - 単位行列
- 対角線要素が1、対角線以外の要素が0である対角行列です
1 0 0
0 1 0
0 0 1 - 対称行列
- 右上要素と左下要素が対象の正方行列です。
1 2 3
2 5 6
3 6 9 - 三角行列
- 右上あるいは左下の要素が0の正方行列です。
1 0 0 1 2 3
4 5 0 0 5 6
7 8 9 0 0 9
下三角行列 上三角行列 - 転置行列
- 行と列を入れ替えた行列です。正方行列である必要はありません。
0 1 2 3 0 10 20
10 11 12 13 ←-→ 1 11 21
20 21 22 23 2 12 22
3 13 23
行列の計算
行列の加減算
for ループを用いて、行列の各要素ごとに計算するならば、どのような計算も可能ですが、行列を単位とした計算では、行列AとBの加減算をするには、双方のサイズが同じでなければなりません。計算は対応する要素間での加減算になります。
A B 計算 A+B
1 2 3 0 1 0 1+0=1 2+1=3 3+0=3 1 3 3
4 5 6 2 0 3 4+2=6 5+0=5 6+3=9 6 5 9
行列の積(内積)
理由を省略して、行列Aと行列Bの積の方法を示します。行列AのサイズをMa×Na、行列BをMb×Nbとしたとき、Na=Mb出なければなりません。C=ABの計算はC[i][j]=ΣA[i][k]・B[k][j] で行い、結果C=ABのサイズはMa×Nbになります。
Bが縦ベクトル(Nb=1)のとき
計算方法
A(3x2) B(2x1) C=AB(3x1)
A[0][0] A[0][1] B[0] A[0][0]×B[0]+A[0][1]×B[1]
A[1][0] A[1][1] B[1] A[1][0]×B[0]+A[1][1]×B[1]
A[2][0] A[2][1] A[2][0]×B[0]+A[2][1]×B[1]
数値例
A B 計算 C
1 2 1 1*1+2*2= 5 5
3 4 2 3*1+4*2=11 11
5 6 5*1+6*2=17 17
Bが行列(Nb=2)のとき
数値例
A(3x2) B(2x2) 計算 C(3x2)
1 2 1 1 1*1+2*2= 5 1*1+2*0=1 5 1
3 4 2 0 3*1+4*2=11 3*1+4*0=3 11 3
5 6 5*1+6*2=17 5*1+6*0=5 17 5
このような計算ですので、AB≠BAです。
逆行列
サイズNの正方行列Aに対して「AB=1(サイズNの単位行列)」となる行列BをAの逆行列といいA-1<.sup>と表記します。BはサイズNの正方行列になります。
計算手順を省略して(注)、数値例を示します。
A B AB
4 2 3 1 0 -1 1 0 0
2 1 1 -3 3 2 0 1 0
3 2 3 1 -2 0 0 0 1
Bの表記をA-1とすれば、AB=AA-1=1のイメージになります。それで逆数との類似により逆行列というのです。
(注)「数学ライブラリ」の「逆行列(トレース版)」で、AあるいはBのデータを入力して「トレース実行」を行ってください。
逆行列の特徴として、BがAの逆行列のときは、AはBの逆行列になります。そしてその積は1なのですから、AA-1=A-1A=1になります。それを使えば、AX=Cの関係があるとき、両辺に右からA-1Aを乗じればA-1AX=A-1C、すなわち X=A-1C となります。この関係は次節で用います。
逆行列と連立方程式
次の連立方程式を考えます。
定数項
4x0+2x1+3x2=10
2x0+1x1+1x2= 4
3x0+2x1+3x2= 9
(この解が1,0,2であることは自明でしょう)
上の式をベクトルで表記すれば、
A X C=AX
4 2 3 x0 10
2 1 1 x1 4
3 2 3 x2 9
となり、X=A-1C の関係があります。
A-1(=B)は、既に知っています。それで、次の計算で簡単に解Xを求めることができます。
A-1 C X
1 0 -1 10 1*10+0*4-1*9=1
-3 3 2 4 -3*10+3*4+2*9=0
1 -2 0 9 1*10-2*4+0*9=2
逆行列を求める計算量は連立方程式を解くのとほぼ同じですから、1回の解を求めるだけではメリットはありません。しかし定数項をいろいろ変更して解を求めたいときは、上のCを配列にした計算をすればよいので、大きなメリットがあります。
固有値、固有ベクトル
かなり高度な数学知識を前提とするので、ここで扱うのは不適切なので省略します。「固有値・固有ベクトル」で簡単な事項を説明しています。