
スタートページ> Web教材一覧> オペレーションズリサーチ> PERT
PDM、プレシデンス・ダイアグラム法、依存関係、リード/ラグ
プレシデンス・ダイアグラム法(Precedence Diagramming Method:PDM)とはPERTの拡張技法の一つで、先行作業と後続作業の依存関係を詳細な指定ができるようにしたものです。
PERTでの表示法には、
AOA記法:作業を矢線で示し、その始点と終点をノードで示す
AON記法:作業をノードで示し、先行・後続関係を矢線で示す
がありますが、PDMはAON図法をベースにしています。
PDMでは、先行作業Pと後続作業Qの間に、4つの依存関係を定義しています。。
「±r」をリード/ラグといいます。
ラグは先行作業に対して後続作業の開始を遅らせる時間(rは)
リードは先行作業に対して後続作業の開始を前倒しする時間(rは-)
(リードの場合。上の説明は複雑になります)
PDMの特別な解法やツールもあるとは思いますが、ここでは次の二つの方法を説明します。
ここでは、次のモデルを解くことにします。簡単にするため「r>0」だけの例を扱います。
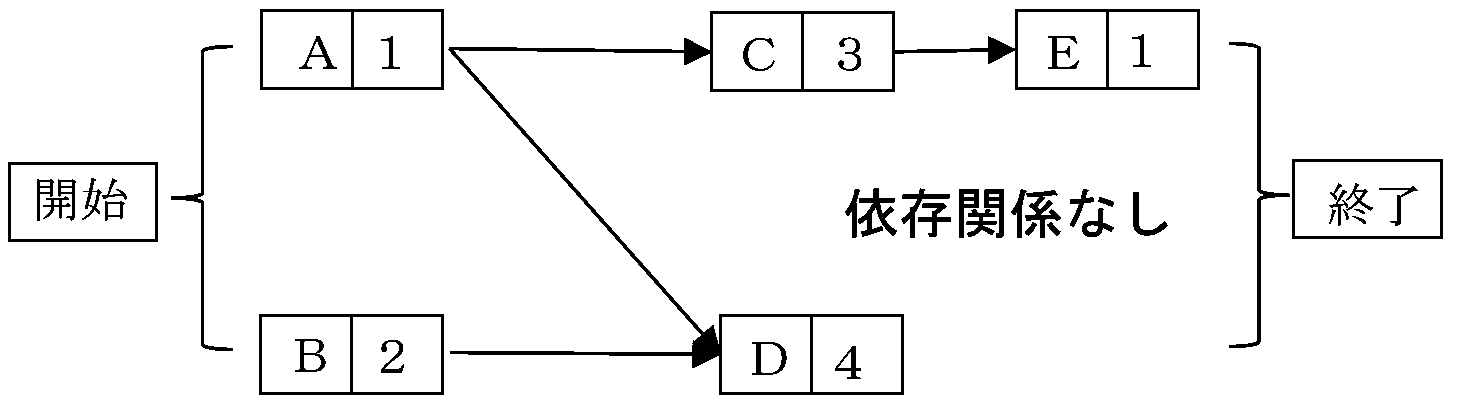
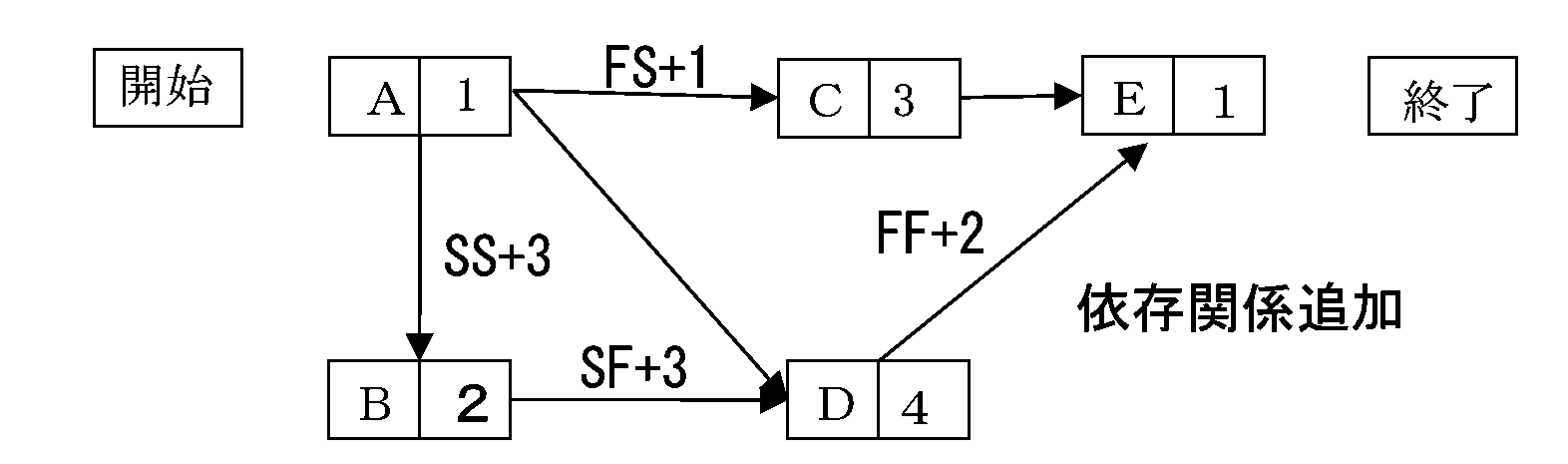
上述の例をPDMの図法で表示すると次のようになります。
この、ES、EF、LS、LFの時刻を、依存関係を考慮して、計算して記入していきます。





LS、LFの計算プロセスは省略しますが、結果は次のようになります。
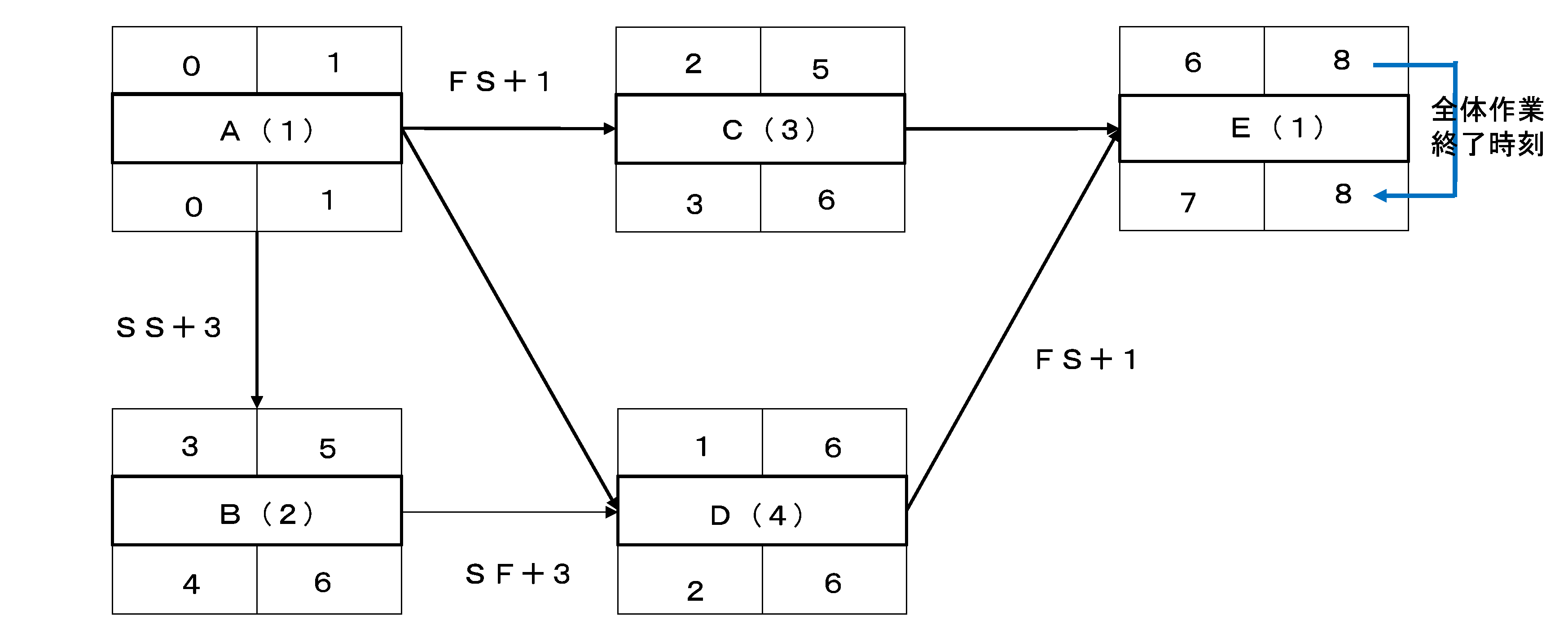
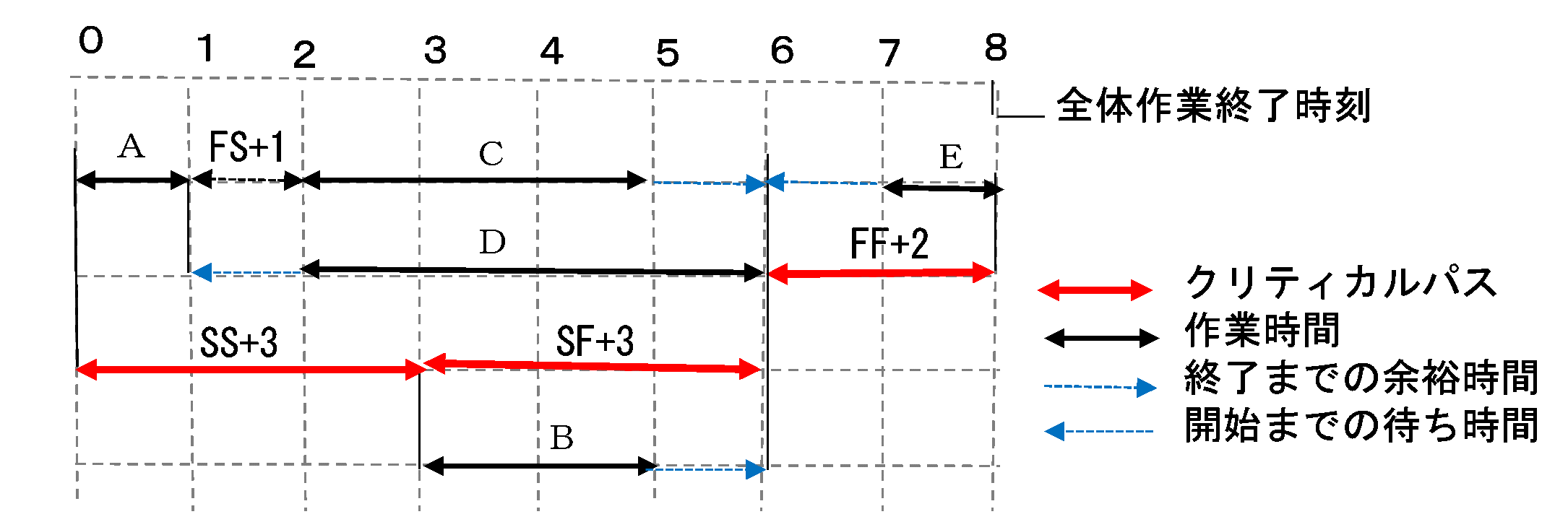
上記の「PDMの解法=通常のAON記法への変換」の例を示します。
右図のようなPDMのモデルを考えます。コンピュータに入力する公式の記法はないのですが、ここでは次の形式にします。
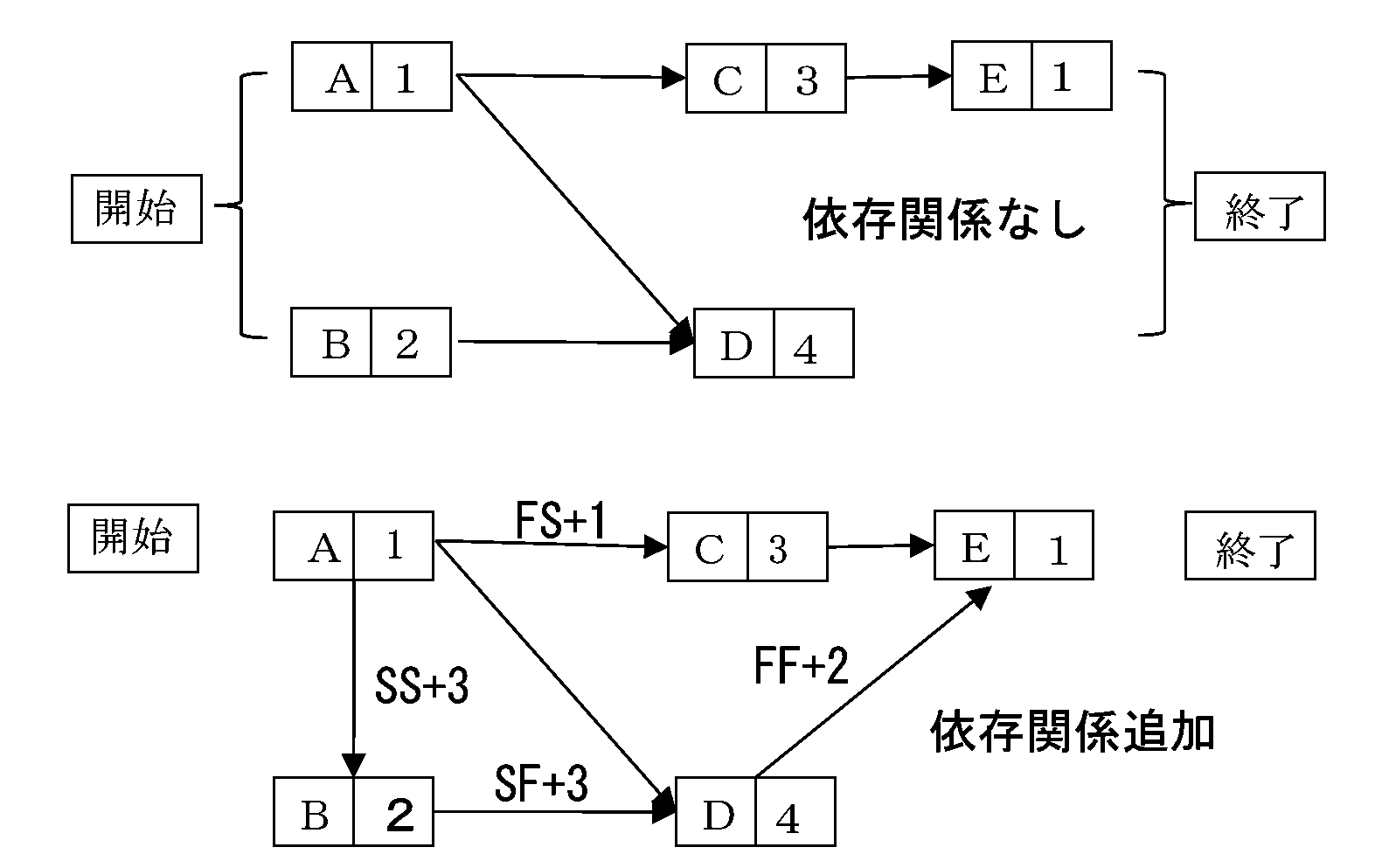
依存関係を無視した(通常のAONモデル)は、「作業名、作業時間、先行作業(リスト)」で記述します。
var 作業表 = [
["A", 1, []],
["B", 2, []],
["C", 3, ["A"]],
["D", 4, ["A","B"]],
["E", 1, ["C"]]
];
依存関係は、「先行作業、後続作業、依存関係、ラグ/リード」の形式で記述します。
var 依存関係 = [
["A", "C", "FS", 1],
["A", "B", "SS", 3],
["B", "D", "SF", 3],
["D", "E", "FF", 2],
];
前述のように、ダミー作業を用いて、依存関係をAONで図示して、それにより作業表を変更します。
本来なら、ダミー作業の名称を指定する必要がありますが、通常はプログラムが自動設定します。ここではア~キとしています。
説明は省略して、AON図は次のようになります。
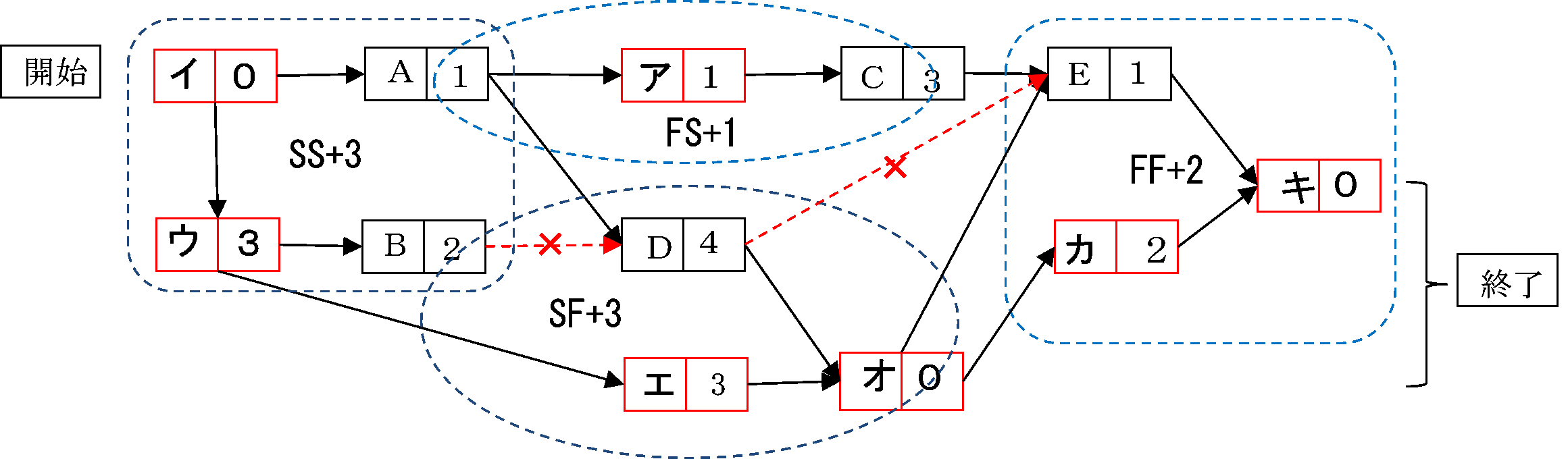
作業Aが終了した1時間後に後続作業Cを開始できます。
通常の作業と同様に、AとCとの間に、作業時間1のダミー作業アを挿入することで、解決できます。
作業表の変更
["ア", 1, ["A"] ] の追加
Cの先行作業のAをアに変更
作業Aが開始してから3時間後に作業Bを開始できます。
「作業Aの開始時刻」が必要になり、作業時間0のダミー作業イを設定します。
イの直後にAを開始するので、Aの先行作業をイとする。
「イから3時間」を、作業時間3のダミー作業ウを設定する。
、
Bの先行作業がウになります。
作業表の変更
["イ", 0, []] の追加
Aの先行作業をイにする
["ウ", 3, ["イ"]] の追加
Bの先行作業をウにする
作業Bが開始してから3時間後に作業Dを終了できる。
=作業Dは、作業B開始後3時間後まで終了できない。
=それまでに終了していたとしても、Dの後続作業は作業B開始後3時間後に開始する。
以前のB→Dの関係は、この依存関係と矛盾するので削除します。
Bの開始時刻は、ウの終了時刻である。ウの後続作業に作業時間3のダミー作業エを設定します。
エの終了時刻はダミー作業オの時刻です。
オをDの後続作業とすれば、オはDとエの終了が遅いほうの時刻になります。
EはDの後続作業でしたが、オまで終了しないので、Eの後続作業になります。
作業表の変更
Dの先行作業からBを削除
["エ", 3, ["ウ"]] の追加
["オ", 0, ["エ","D"]] の追加
Eの先行作業Dの削除
Eの先行作業オの追加
作業D終了の2時間後に作業Eを終了できる。
=作業Dの終了時刻はオであるから、オの2時間後まではEは終了できない。
「オの2時間後」のために、作業時間2のダミー作業カを設定
さらに、カの終了時刻として、作業時間0のダミー作業キを設定。
これにより、作業Eの終了時刻はキとなります。
作業表の変更
Eの先行作業からDを削除
Eの先行作業にオを追加
["カ", 2, ["オ"]] の追加
["キ", 0, ["カ","E"]] の追加

作業表
作業 所要 先行
名 期間 作業
A 1 イ
B 2 ウ
C 3 ア
D 4 A
E 1 C、オ
ア 1 A
イ 0
ウ 3 イ
エ 3 ウ
オ 0 D、エ
カ 2 オ
キ 0 E、カ
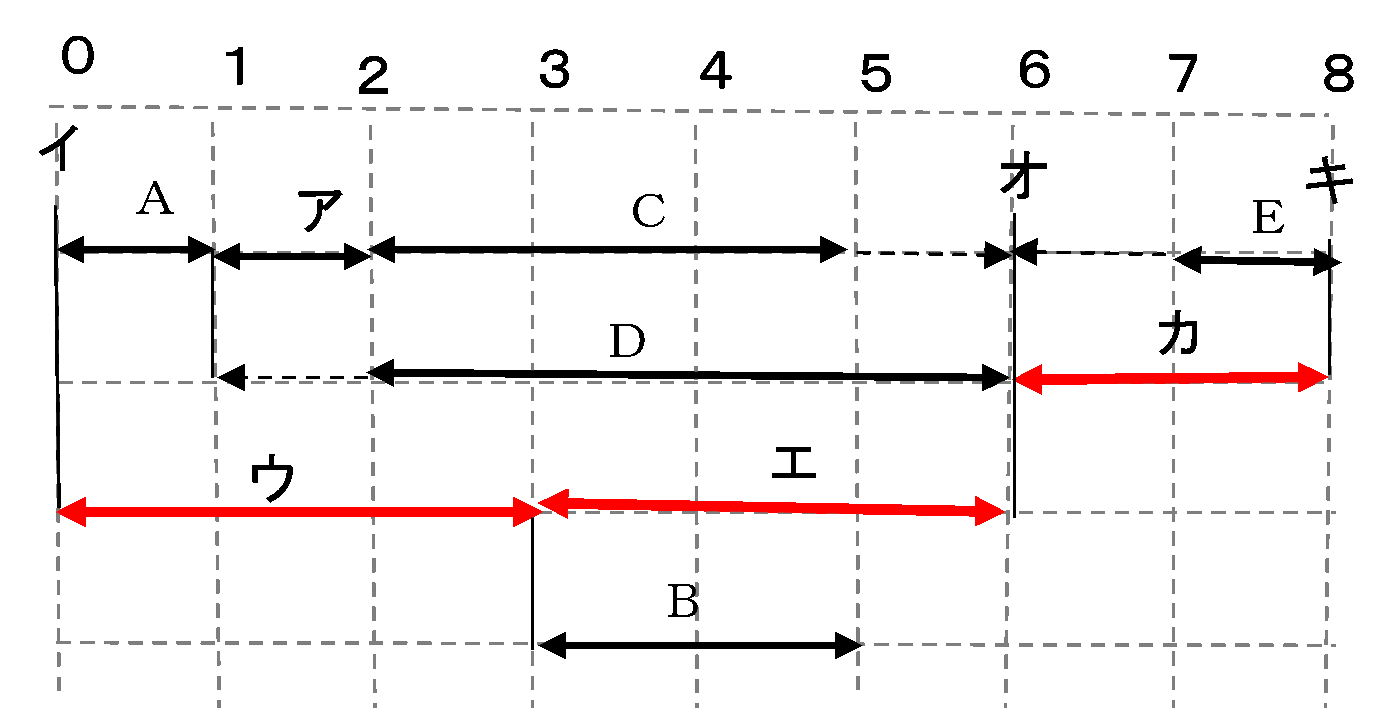
AONでのPERTの計算プログラムを実行した結果は次のようになりました。
●rtn["作業表"][i][*] 作業 作業 先行作業 後続作業 最早日 最遅日 余裕 名 日数 個数 作業 個数 作業 開始 終了 開始 終了 日数 イ 0 0 2 A、ウ 0 0 0 0 0 A 1 1 イ 2 D、ア 0 1 1 2 1 ウ 3 1 イ 2 B、エ 0 3 0 3 0 ア 1 1 A 1 C 1 2 3 4 2 D 4 1 A 1 オ 1 5 2 6 1 C 3 1 ア 1 E 2 5 4 7 2 B 2 1 ウ 0 3 5 6 8 3 エ 3 1 ウ 1 オ 3 6 3 6 0 オ 0 2 D、エ 2 E,カ 6 6 6 6 0 E 1 2 C、オ 1 キ 6 7 7 8 1 カ 2 1 オ 1 キ 6 8 6 8 0 キ 0 2 E、カ 0 8 8 8 8 0 ●rtn["全所要日数"] = 8 ●rtn["クリティカルパス"][*]=イ,ウ,エ,オ,カ,キ
[記号]は私が勝手につけたものです。依存関係が同じでもリードやラグ(r)の値により対応が異なるからです。
[依存関係][意味][ガントチャート]については、説明は不要でしょう、
[AON図法」は、依存関係をAON記法で図にしたものです。
[作業表の変更]は、AON図法を作業表の変更内容を具体的に説明したものです。
AON記法では、「ノード名、作業時間、先行作業」の形式で表現するので、変更操作もそれに合わせる必要があります。




「作業表」と「依存関係表」を与えたときに、変換後のAON作業表を作成するプログラムです。