補間（ラグランジュの補間公式、ニュートンの補間公式）

補間とは

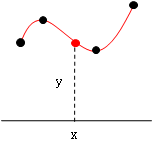
右図のように、ｎ＋１個の点（黒点）(x₀,y₀),(x₁,y₁),(x₂,y₂),・・・,(x_n,y_n)が与えられているとき、その点を通るなめらかな曲線をひき、x₀～x_nの間の値ｘにおける点（赤点）のｙの値を求めることを補間といいます。
　ｎ＋１個の点を通る曲線は多様ですが、最も単純なのはｎ次の多項式、
　　　ｙ＝c₀＋c₁x＋c₂x²＋・・・＋a_nxⁿ
です。
　すなわち、補間とは、この係数 c_r を算出してｎ次多項式 f(x) を決定し、与えられた x=x_* における f(x_*) を求めることです。

連立方程式による係数の決定法

ｎ＋１個の点を通るｎ次多項式の係数は、連立方程式により求めることができます。点 (x_k,y_k) を通ることは、
　　y_k＝c₀ + c₁x + c₂x² + … + c_nxⁿ　　（k=0～n）
で表せます。

４つの点(0,1), (2,5), (3,8), (5,10)がを通る３次式ならば、
(0, 1)：　1 = c₀ + 0*c₁ +　0*c₂ +　 0*c₃
(2, 5)：　5 = c₀ + 2*c₁ +　4*c₂ +　 8*c₃
(3, 8)：　8 = c₀ + 3*c₁ +　9*c₂ +　27*c₃
(5,10)： 10 = c₀ + 5*c₁ + 25*c₂ + 125*c₃
を解くことにより、
　　 c₀ = 1, c₁ = 0.133, c₂ = 1.333, c₀ = -0.2
となるので、３次式は、 　　y = 1 + 0.133x + 1.333x² - 0.2x³
となります。

しかし、この方法では、点の数（次元）が大きくなると、解くための計算量が大きくなるだけでなく、誤差が累積する欠点があります。
　それを回避する代表的な方法に、ラグランジュの補間公式、ニュートンの補間公式があります。

補間での留意点

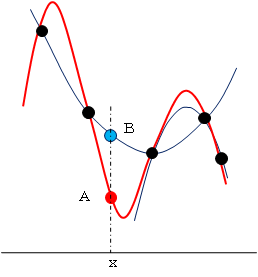
ｎ＋１個の点をｎ次式で補間するとき、ｎが大きくなると、右図（赤線、点Ａ）のように、実際とは異なるのではないかと思われる補間値になることがあります。特に、x_* が x₀～x_n の外側の場合（外挿という）には、そうなることが多いのです。

このような欠点を回避するには、あえて全体を一つの式で表すのではなく、補間すべき周辺の数点だけを用いて、低次元の式（青線）で補間を行う（Ｂ点）ことがよく行われます。その代表的な方法にスプライン補間公式があります。しかし、この方法は数学的にも高度ですし、計算も複雑になるので、ここでは省略します。→参照：「スプライン補間」

なお、補間と似たような手法に最小二乗法があります。最小二乗法は、「すべての点を通る」という補間の原則を放棄して、「すべての点に近い」低次元の多項式で近似することにより、極端な補間値を避ける方法だということもできます。

１次式での補間

ラグランジュの補間多項式の前に、２点(x₀,y₀),(x₁,y₁)が与えられ、１次式により、x₀～x₁の間にあるｘに対するｙを求める場合を考えます。

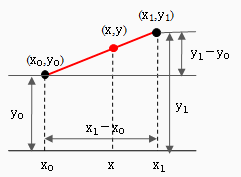
２点(x₀,y₀),(x₁,y₁)を通る直線は、
　　　y＝ (y₁－y₀)/(x₁－x₀) * (x－x₀) ＋ y₀
です。これを変形すると、次の式が得られます。
　　　y＝ (x－x₁)/(x₀－x₁)*y₀ + (x－x₀)/(x₁－x₀)*y₁

例えば、２点を(１,３)と(４,７)とし、ｘ＝３とすると、
　　(x－x₁)/(x₀－x₁)*y₀＝(3-4)/(1-4)*1＝ 1/3
　　(x－x₀)/(x₁－x₀)*y₁＝(3-1)/(4-1)*7＝14/3
ですから、
　　y＝ 1/3 + 14/3 ＝ 5
になります。

ラグランジュの補間多項式

ｎ次式に一般化して、
　　　ｙ＝c₀y₀＋c₁y₁＋c₂y₂＋・・・＋c_ny_n
としたときの、c_kは、次の式になります。
　　c_k = (x-x₀)/(x_k-x₀) * (x-x₁)/(x_k-x₁) * … * (x-x_k-1)/(x_k-x_k-1)
　　　　　　　　　　（(x-x_k)/(x_k-x_k)の項がないことに注意）
　　　 * (x-x_k+1)/(x_k-x_k+1) * … * (x-x_n)/(x_k-x_n)

例えば２点、１次式のときはｎ＝１ですから、上の式でx₂以上のものがある項は不要です。それで、
　　c_k = (x-x₀)/(x_k-x₀) * (x-x₁)/(x_k-x₁)
となり、「(x-x_k)/(x_k-x_k)の項がない」ことから
　　c₀ = (x-x₁)/(x₀-x₁)
　　c₁ = (x-x₀)/(x₁-x₀)
となるので、１次式、
　　y = (x-x₁)/(x₀-x₁)*y₀ + (x-x₀)/(x₁-x₀)*y₁
が得られます。これは、前述の「１次式での補間」で示した結果と一致します。

数値例

４つの点(0,1), (2,5), (3,8), (5,10)が与えられ、それを通る３次式を求めます。
　　x₀=0, 　x₁=2, 　x₂=3, 　x₃=5
　　y₀=1, 　y₁=5, 　y₂=8, 　y₃=10

c₀ = 　　　　　　　　(x-x₁)/(x₀-x₁) * (x-x₂)/(x₀-x₂) * (x-x₃)/(x₀-x₃)
c₁ = (x-x₀)/(x₁-x₀) 　　　　　　　 * (x-x₂)/(x₁-x₂) * (x-x₃)/(x₁-x₃)
c₂ = (x-x₀)/(x₂-x₀) * (x-x₁)/(x₂-x₁) 　　　　　　　 * (x-x₃)/(x₂-x₃)
c₃ = (x-x₀)/(x₃-x₀) * (x-x₁)/(x₃-x₁) * (x-x₂)/(x₃-x₂)

y = c₀y₀ + c₁y₁ + c₂y₂ + c₃y₃

ｘ＝４のときは、
c₀y₀ = [　　　2/(-2) * 1/(-3) * (-1)/(-5)]* 1 = 0.067
c₁y₁ = [4/2　　　　　* 1/(-1) * (-1)/(-3)]* 5 = -3.333
c₂y₂ = [4/3 * 2/1　　　　　　 * (-1)/(-2)]* 8 = 10.667
c₃y₃ = [4/5 * 2/3　　* 1/2　　　　　　　 ]*10 = 2.667

y = f(4) = 0.067 - 3.333 + 10.667 + 2.667 = 10.07

ニュートンの補間公式

n+1個の点(x₀,y₀), (x₁,y₁), ・・・,(x_n,y_n)を通るｎ次式 f(x)を、
　　　ｆ(x)＝ｃ₀ ＋ ｃ₁(x-x₀) ＋ ｃ₂(x-x₀)(x-x₁)
　　　　　　　＋ ・・・ ＋ ｃ_n(x-x₀)(x-x₁)・・・(x-x_n-1）
の形で表します。
　そして、
　　　ｆ(x₀)＝y₀、ｆ(x₁)＝y₁、・・・、ｆ(x_n+1)＝y_n+1
の関係から、ｃの値を求めて、ｎ次式 ｆ(x) を決定します。

例示

ｎ＝3とし、４つの点を(0,1), (2,5), (3,8), (5,10)としましょう。
　上の公式は次のようになります。
　　　ｆ(x)＝ｃ₀ ＋ ｃ₁(x-0) ＋ ｃ₂(x-0)(x-2) ＋ ｃ₃(x-0)(x-2)(x-3))
　そして、ｆ(0)＝y₀＝1, ｆ(2)＝y₁＝5, ｆ(3)＝y₂＝8, ｆ(5)＝y₃＝10 です。

• ｃ₀：ｆ(x₀)＝ｃ₀＝y₀
  →　ｃ₀＝1
• ｃ₁：ｆ(x₁)＝ｃ₀ ＋ ｃ₁(x₁-x₀)＝y₁
  →　1 + ｃ₁(2-0)＝5
  → ｃ₁＝2
• ｃ₂：ｆ(x₂)＝ｃ₀　+ ｃ₁(x₂-x₀) + ｃ₂(x₂-x₀)(x₂-x₁)＝y₂
  → 1 + 2(3-0) + ｃ₂(3-0)(3-2)＝8 → 1 + 6 + ｃ₂*3＝ 8
  → ｃ₂＝1/3
  
• ｃ₃：ｆ(x₃)＝ｃ₀ + ｃ₁(x₃-x₀)　+ ｃ₂(x₃-x₀)(x₃-x₁) + ｃ₃(x₃-x₀)(x₃-x₁)(x₃-x₂)＝y₃
  → 1 + 2(5-0) + 1/3(5-0)(5-2) + ｃ₃(5-0)(5-2)(5-3)＝10
  → 1 + 10 + 5 + ｃ₃30＝10
  → ｃ₃＝-1/5

これより、
　　　ｆ(x)＝1 + 2*(x-0) + 1/3*(x-0)(x-2) + (-1/5)*(x-0)(x-2)(x-3)
が得られます。

これから、ｘ＝４のときを求めれば
　　　ｆ(4)＝1 + 2*(4-0) + 1/3*(4-0)(4-2) + (-1/5)*(4-0)(4-2)(4-3)＝ 10.07
となります。
　これは、ラグランジュの補間公式での結果と一致します。それは当然のことで、両者の数値例での見かけの式は異なりますが、　y＝c₀ + c₁x + c₂x² + c₃x³ の形式に整理すれば、「連立方程式」で求めた
　　y = 1 + 0.133x + 1.333x² - 0.2x³
になっているのです。

差分による説明

ｃ_rは、次の差分表を作ると、簡単にに計算できます。

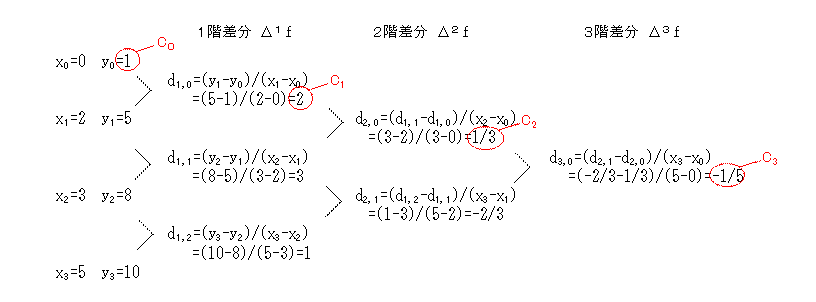
ｎ次式の係数 c_r は、c_r＝d_r,0になります。
　そして、d_r,k は、次の式で計算できます。
　　d_r,k＝(d_r-1,k+1-d_r-1,k)/(x_r+k-x_k) 　　ただし、r＝1～n　　ｋ＝0～n-r　　d_0,k＝y_k

ここで、ｄ_1,0は、 (x₀,y₀) と (x₁,y₁) の傾きですから、ｆ(x) を微分したものになります（階差分商といいます）。ｄ_1,1、ｄ_1,2 も同様です。
　また、ｄ_2,0 は、（x₀,d_1,0) と (x₂,d_1,1) の傾きだといえるので、ｄ_2,0は、ｆ(x) を２回微分したものだといえます。ｄ_3,0は、３回微分したものになります。
　すなわち、d_r,k は、点 (x_k,y_k）を起点とするｒ階の階差分商であり、ニュートンの補間法の公式は、階差分商を係数にした多項式だといえます。

ラグランジュの補間とニュートンの補間の比較

• ラグランジュの補間は計算が簡単で誤差累積が少ない
  ラグランジュの補間は、(x-x_i)/(x_j-x_i) の繰り返しです。入力データからの直接の計算ですので、計算そのものが単純です。
  ニュートンの補間は、ｄ_r,k の計算が必要で、入力データを計算した値をさらに計算することになります。その回数（階数）が大きくなると誤差が累積することがあります。
• ニュートンの補間は点の追加による再計算が容易
  計算例では４個の点でしたが、それに５番目の点（x₅＞x₄） が追加されたとします。ラグランジュの補間では、c_iの計算すべてに影響します。それに対してニュートンの補間では、ｃ₄までには影響せず、ｃ₅だけを追加すればよいことになります。そのため、４個までのときの補間計算結果を蓄えておけば、５番目の点が加わったときに、それを再利用できます。

計算プログラム