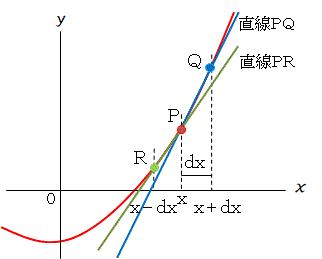
前進差分近似
微分とは、曲線 y=f(x)の傾きを求めることです。
右図でP点(x=x)の傾きはP点の接線のx項の係数であり、その接線は、P点とQ点(x=x+dx、dxは小さい値)を通る直線PQの傾きで近似できます。すなわち、、
\[
\frac{df}{dx}
= \lim_{dx \to 0}
\frac{f(x+ dx)-f(x)}{dx}
\]
で定義されます。
同様に、dx=0.01とすれば、2.01になります。
私たちは、\( y=f(x)=x^2-0.5 \) の微分は\( \frac{df}{dx}=2x \) なので、x=1 のときは2であることを知っています。dxが小さくなるほど、2に近づきます。
後退差分近似
P点の傾きは、直線PRで近似することもできます。そのときは(dx=0.1)ならば \[ \frac{df}{dx} = \lim_{dx \to 0} \frac{f(x)-f(x-dx)}{dx} =\frac{f(1)-f(0.9)}{0.1} =\frac{0.5-0.31}{0.1} =1.9 \] になります。
中心差分近似
一般には、前進差分近似を使うことが多いのですが、前進差分近似と後退差分近似の平均のほうが近似がよいと考えられます(dxに比較して大した効果はないが)。 \[ \frac{df}{dx} = \lim_{dx \to 0} \frac{f(x+dx)-f(x-dx)}{2dx} =\frac{f(1.1)-f(0.9)}{0.2} =\frac{0.71-0.31}{0.2} =2 \]