スタートページ＞ Javascript＞ ＣＡＮＶＡＳ＞ 物理等

物理　力学　減衰振動

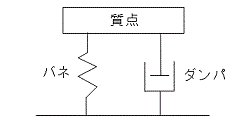
図のように、質点－ダンパ－バネで構成されるシステムがあります。
質点を少し上にあげて手を離すと、振動しながら一定の点に近づき止まります。
（そのようになるように、ダンパとバネを設定したいのです。）

バネが弱いとダンパだけになりすぐに安定します。
ダンパが弱いとバネだけになり振動が続きます。
適切に選ぶと次第に振幅が小さくなります。

いろいろ変えて実験してください、

cm:ダンパ特性 　km:バネ特性
x0:初期位置 　x'0:初期速度

（解説）

理論と解説

x(t) の１階微分を x'(t), ２階微分を x"(t) と表現することにします。
物体の質量ｍ[kg]、ダンパーの減衰係数ｃ[Ns/m], バネ係数ｋ[N/s] とすると、
物体の時刻ｔにおける位置ｘは、運動方程式
　　　m*x"(t) + c*x'(t) + k*x(t) = F (外力、ここでは０とします） で表せます。

いくつかの物理量
ｗ = √(k/m)：固有角振動数
γ = c/(2m)：
ζ = γ/ｗ：減衰比
wd = √(γ2 - ｗ）(γ>w),　√(ｗ2 - γ2）(γ<ｗ)
λ1 = -γ+ wd, λ2 = -γ- wd: 　　上の運動方程式を　λ2 + (c/m)λ + (k/m) = 0 としたときの解

運動方程式の解

２階微分方程式ですから、一般解は未定の２つの定数項 A, B を持ちます。時刻での物体の位置 x(0) と速度 x'(0) が既知だとして、A, B を特定します。

タイプ１　γ = 0 (c=0：ダンパなし)　減衰しない
　一般解：x(t) = A*sin(wt) + B*cos(wt)
　初期条件：x(0)=B, x'(0)=w*A → A = x'(0)/w, B = x(0)

タイプ２　γ > w (λが実根, ζ>1)　過減衰
　一般解：x(t) = A*eλ1t + B*eλ1t
　初期条件：x(0)=A+B, x'(0)=λ1*A +λ2*B→ A = (λ2x(0)-x'(0))/(-2wd), B = (λ1x(0)-x'(0))/(2wd)

タイプ３　γ = w (λが重根, λ1=λ2)
　一般解：x(t) = e-γｔ*(A + B*t)
　初期条件：x(0)=A, x'(0)=-γA +B → A = x(0), B = x(0)+γx'(0)

タイプ４　γ < w (λが複素根,ζ<1) 減衰振動
　一般解：x(t) = e-γｔ*(A*sin(wdt) + B*cos(wdt)
　初期条件：x(0)=B, x'(0)=B+-γA +B → A = (x(0)-x'(0))/wd, B = x(0)