物理　力学　二重振子

解説

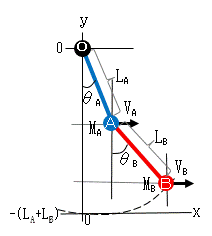
現在の青Ａと赤Ｂの座標
　　XA =  LA*sin(θA)
    YA = -LA*cos(θA)
    XB =  LA*sin(θA) + LB*sin(θB)
    YB = -LA*cos(θA) - LB*cos(θB)
位置エネルギー　Ｕ
　　Ｕ = (MA + MB)*g*LA*(1-cos(θA) + MB*g*LB(1-cos(θB)

角速度
　　dθA =  LA*sin(θA)
    dθA = -LA*cos(θA)
    dθB =  LA*sin(θA) + LB*sin(θB)
    dθB = -LA*cos(θA) - LB*cos(θB)
ＸＹ座標では
    VA2 = (LA*dθA)2
    VB2 = (LA*dθA)2 + (LB*dθB)2 +2LALBdθAdθB*cos(θA - θB)
運動エネルギー　Ｔ
　　Ｔ = (1/2)MA*VA2 +  (1/2)MB*VB2
       = (1/2)(MA+MB)*(LA*dθA)2 + (1/2)MB*(LB*dθB)2 + MB*LAdθA*LBdθB*(cos(θA-θB)

ラグランジアン Ｌ = ＴーＵ
　　Ｌ = (1/2)(MA+MB)*(LA*dθA)2 + (1/2)MB*(LB*dθB)2 + MB*LAdθA*LBdθB*(cos(θA-θB)
        -(MA+MB)*g*LA*(1-cos(θA)) - MB*g*LB(1-cos(θB)

　★式を簡単にするために、LA = LB = L, MA = MB = M とする
　　Ｌ = (M*L2)*(dθA2+(1/2)dθB2+ dθAdθB(cos(θA-θB))
       + MgL(2cos(θA) + cos(θB) - 3)

ラグランジュの運動方程式
    θの２階微分　d(dθA)/dt = ddθA,　d(dθB)/dt = ddθB と表記する

    d ┌∂Ｌ┐　∂Ｌ
　　─│──│－──  ＝０　
　　dt└∂ｔ┘　∂θA
　　→　ML2{2*ddθA + cos(θA-θB)*ddθB + sin(θA-θB)*dB2 + (2g/L)sin(θa) } = 0

    d ┌∂Ｌ┐　∂Ｌ
　　─│──│－──  ＝０　
　　dt└∂ｔ┘　∂θB
    →　ML2{ddθB + cos(θA-θB)*ddθB - sin(θA-θB)dθA2 + (g/L)sin(θB) } = 0

　　ddθA, ddθB を変数とした行列の形式にする C = cos(θA-θB)
　　　┌2, C┐┌ddθA┐＝┌D1┐ 　-sin(θA-θB)*dθB2 - (2g/L)sin(θA)　
　　　└C. 1┘└ddθB┘　└D2┘    sin(θA-θB)*dθA2 - (g/L)sin(θB)

この連立方程式を解くには、計算精度の観点では、ルンゲ・クッタ法がよいのですが、単純のためにオイラー法を用います。
　次のように漸化式に形式にして、係数Ａ、Ｂを求めます。
　　Ｃ = cos(θA-θB)  ①
    Ｄ1 = -sin(θA-θB)*dθB2 - (2g/L)sin(θA)    
    Ｄ2 =  sin(θA-θB)*dθA2 - (g/L)sin(θB)

　　dθA(t+dt) = dθA(t) + Ａ*dt　②　　Ａ = (D1-C)/(2-C2)
　　dθB(t+dt) = dθB(t) + Ｂ*dt　　　　Ｂ = (2D2-CD1)/(2-C2)
　　θA(t+dt) = θA(t) + dθA(t)*dt　③
　　θB(t+dt) = θB(t) + dθB(t)*dt

　このときの青点・赤点の位置　（L=1 とする）
　　XA(t+dt) =  sin(θA(t+dt))        ④
    YA(t+dt) = -cos(θA(t+dt))
    XB(t+dt) =  sin(θA(t+dt)) + sin(θB(t+dt))
    YB(t+dt) = -cos(θA(t+dt)) - cos(θB(t+dt))

シミュレーション
　　初期値
        g/L = 1 (適当に設定する）
        角度　　θA(0),  θB(0)
　　　　角速度 dθA(0), dθB(0)
　　① Ｃ、Ｄ1, Ｄ2 の計算
　　②　dθA(t+dt), dθB(t+dt) の計算　（θの変化勾配）
　　③　θA(t+dt), θB(t+dt) の計算
　　④　t+dt での青点・赤点のＸＹ座標が分かるので、画像に表示する
　　①～④を繰り返すことにより、点の動きが表示できる。