スタートページ> Javascript> CANVAS> 物理等
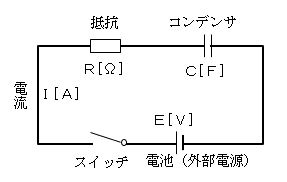
右図の直流回路において、t=0でスイッチを入れ、t=Toff で切り、、t=Ton でまたスイッチを入れたとき、時間tにおける電流 I、コンデンサの電荷Cの変化を図示します。
主要諸元 固定値の諸元 起電力 E 10v 電池(外部電源)の電圧。期間中一定 抵抗 R 5Ω 期間中一定 コンデンサ Cmax 10v コンデンサの最大容量 時刻tにおける諸元 コンデンサ容量 C(t) 電流 I(t) スイッチ操作時刻 切断時刻 Toff 10 程度が適切 再接続時刻 Ton Toff+5 程度が適切解説
t=0 のとき、電池の電位E=E0、コンデンサの電位C=0
充電が完了したときの時刻 t=Tのとき、電池の電位E=E-C、コンデンサの電位C=C0
になりますが。その間は直線的に変化するのではありません。
私は、この分野の知識がないので、勝手に次のように考えました。
電池とコンデンサの電位差によるので、指数関数になります。
t=t における確率密度 p = λ*e(-λ*t) コンデンサの充電速度
区間 t=0~t の累積確率 s = 1-e(-λ*t) tにおけるコンデンサの電位
累積確率が p となる t の値 t = -(1/λ)log(1-p) コンデンサ指定電位になるまでの時間
取扱の都合により、p=0.99 (充電終了とみなす)の時刻 Toff を 10 程度になるようにλを設定したいのです。
λ = -(1/t)log(1-p) = -0.1log(0.01) = 0.46
これより、コンデンサの容量をCmax, tにおける電位をC(t) とすれば
C(t) = Cmax(1-e-0.46t) ( )内>0,99 ならばC(t) = Cmax
となります。
抵抗Rがあり、コンデンサの電位がC(t). 電池の電位がE(t)のときの電流 I(t) は、
I(t) = (E - C(t)) / R
となります。