バスタブ曲線(bath-tub curve)
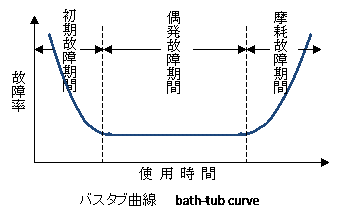
製品を使用するときの故障率の時間推移は右図のようになります。その形状からバスタブ曲線といいます。
- 初期故障確率
- 導入当初は部品の不良や調整の不良による故障が発生しますが、取替や修正により、時間とともに故障確率は減少します。
- 偶発故障確率
- 初期故障がほとんどなくなると安定状態になります。しかし、偶発的な故障は発生しますので、故障率は一定の値になります。
- 摩耗故障確率
- 長期間使用していると、部品の劣化が起こり、時間とともに故障が多くなります。
このような故障の推移は、多様な分野で見られます。生物学では、生物は幼児期の死亡率は高いが次第に減少し、青年・成年期には安定し、老齢になるに従い死亡率が高くなります。情報システムでは、導入当初はプログラムミスや利用上の不都合などが発生しますが、修正することにより次第に安定します。しかし、そのうちに業務の変化やITの発展により、システムの改善要求が高まり、最後に全面改訂になります。
ワイブル分布(Weibull distribution)
ワイブル分布は、上述の3つの故障確率を数式化するのに適した確率分布です。この分布を組み合わせることにより、バスタブ曲線を数学的に記述し、多様な分析を行うことができます。
ワイブル分布は、次のように表現されます。
β:形状パラメタ(分布の形)ワイブル係数
η:尺度パラメタ(時間のスケール)
確率密度関数:時刻tまで故障せず時刻tで故障する確率
f(t) = (β/η)(t/η)β-1e-(t/η)β
└─┬───────┘└─┬──┘
│ R(t) = e-(t/η)β 時刻tまでに故障しない確率
h(t) = (β/η)(t/η)β-1 時刻tで故障する確率
累積分布関数:時刻tまでに故障する確率
F(t) = 1-R(t) = 1-e-(t/η)β
式の説明
簡潔のため、上の式を η=1 にしたもので説明します。さらに、β=1とするとワイブル分布は指数分布(平均λ=1/η=1)になります。すなわち、ワイブル分布は指数分布を拡張したものなのです。
1 tβ-1 1
h(t) = βtβ-1、 R(t) = ───、 f(t) = β───、 F(t) = 1-───
etβ etβ etβ
β=1のとき
h(t) = 1、 R(t) = e-t、 f(t) = e-t、 F(t) = 1-e-t
h(t):故障分布関数(failure rate function)
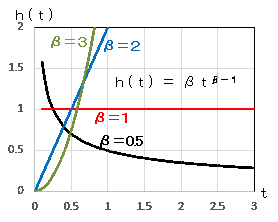
ハザード関数(hazard function)ともいいます(ハザードは「潜在的危険性」)。
時刻tまでに故障したことがあるか否かに関係なく、時刻tで故障が発生する確率密度です。いいかえれば、時刻tまで故障しなかったという条件のもとで、その時間に故障する条件付き確率密度です。
- β=1:一様分布になります。時刻tに関係なく故障は同確率で発生します。偶発故障確率に利用できます。
- 0<β<1:次第に緩やかになる右下がりの曲線になります。初期故障確率に利用できます。
- 1<β:次第に急になる右上がりの曲線でβが大になると急激に増大します。グラフを右に移動すると、摩耗故障確率に利用できます。
このように、ハザード分布での故障分布関数を時刻帯によりβを変えることにより、バスタブ曲線を生成することができます(厳密には複雑な処理が必要ですが)。
R(t):信頼度関数(reliability function)
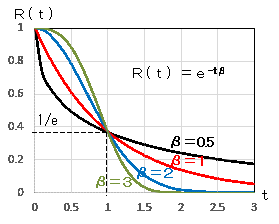
時刻tまで故障しない累積確率です。β=1のグラフでt=2のとき、R(2)=0.135になります。これは、「t=2までに故障が起きない確率は13.5%だ」ということです。
当然ですが、t=0の瞬間では故障がないので確率は1です。時間が経てばその間に故障が発生する確率は大きくなるので、βに関係なく右下がりになります。また、各グラフの下側の面積は1ですので、左側で大のときは右側で小になります。
生物学で「故障=死亡」だとすれば、R(t) は「時刻tまで死んでいない確率」すなわち、「時刻tまで生きている確率」になります。それでR(t)をS(t):生存関数 (survival function)といいます。
f(t):確率密度関数(probability density function、PDF)

f(t) =h(t)×R(t)
=「時刻tに故障が起こる確率」×「時刻tまでに故障が起こらない確率」
=「時刻tで最初の故障が起こる確率」
・β≦1のときは、t=0で最大。その後小さくなります。最初の故障は使用直後が最も起こりやすくなります。
・1<βのときは、山形になりβ=2では0.7、β=3では0.9付近で最初の故障が最も起こりやすくなります。
F(t):累積分布関数(cumulative distribution function, CDF)
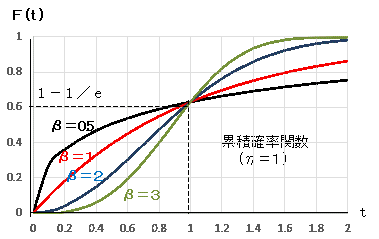
定義としては、f(t) を0からtまで積分したものです。時刻tまでに最初の故障が起こる確率です。
また、F(t) = 1-R(t) の関係があります。R(t) は「時刻tまでに故障が起こらない確率」ですから、これからも「時刻tまでに最初の故障が起こる確率」になります。
補足
スケールとシフト
ここまで、η=1として説明してきました。それを復活します。また、これまで触れてきませんでしたが、t→t-τと置き換えると、τは位置パラメタになります。
ここでは、f(t):確率密度関数(β=2)を例にして説明します。
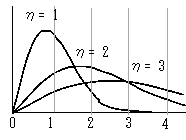
- η:尺度パラメータ(左図)
- t→(t/η)の変換では、t=1 が t=η になるのですから、横にη倍に引伸ばすことになります。そして面積=1ですから、高さは 1/η 倍に縮小されます。
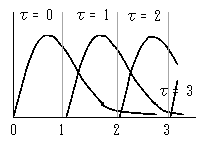
- τ:位置パラメータ(右図)
- t→(t-τ)の変換では、t=0がt=τになるのですから、τだけ右に平行移動したものになります。
β:形状パラメタ
他の分布との関係
・β=1:指数分布
・β=2:レイリー分布
・β→大:正規分布に近づく(f(t) のグラフ参照)
Rayleigh分布は、通信工学の分野で、入力屈折損失、変調側波帯注入、搬送波抑圧、RF減衰の測定などの測定データを表すためによく使用されます。また、この分布は電子真空装置の寿命試験にもよく使用されます。
実務ではβの値をどう決めるかが重要です。厳密には複雑な計算になりますが、一般には次のような手順で行います。
・類似製品あるいは過去の記録から、故障率などのデータをヒストグラムに作成します。
・それをワイブル確率紙という特殊な方眼紙にプロットします。
・直線になっていれば、ワイブル分布に従っていることになります。
・その傾きなどからβを読み取ります。
ワイブル分布からバスタブ曲線へ
「h(t):故障分布関数」で簡単に述べましたが、実際には「形が似ている」程度のことで近似することはできません。特に期間の移行点の物理的・実務的意味付けや曲線の接続に関する検討が必要ですし、複雑な計算(ワイブル確率紙などのツールの活用)を伴います。かなり専門的になりますので割愛します。