本章の内容
本章では「ＡＩ（人工知能）」の技法のうち、「分類問題」を「教師あり」の「階層型ニューロネットワークモデル」でアプローチする方法の概要をテーマにします。
- 分類問題
いくつかの特性を持つデータが、どのグループに属するかを求める問題です。会員申請者の特性から会員にするか／しないかを決めたり、手書き数字を与えて０～９のどれかを決定するなどがあります。 - 教師あり問題
多くのデータに人間が与えたラベル（正解：会員にする、５であるなど）を与えることにより、データの特性からラベルに一致する率（正解率）を最大にするようなルールを探す問題です。 - 階層型ニューロネットワークモデル
そのルールを探すには、従来のアプローチは、人間が統計的方法を用いて試行錯誤で最適なルールを作成していました（左図）。
それに対して階層型ニューロネットワークモデル（右図）のように、人間の脳を模倣したニューロンとシナプスからなるネットワークを設定し、次のニューロンに伝播する「重さ」をシステムに任せようとするアプローチです。なお、ニューロネットワークモデルというとき、階層型を指すのが通常です。
実際のニューロネットワークモデルでは、多数の特性を持つ膨大なデータが必要であり、中間層の段数も各層のニューロン数も多くなります。ここでは考え方の紹介が主目的ですので、極めて単純なモデルにします。そのため、不適切なモデルであったり、正解率が低かったりすることには考慮しないことにします。
関連ページ
- 機械学習
人工知能の概要や体系など - ニューロコンピュータ
ニューロコンピュータのやや詳細な説明です。 - ニューロコンピュータ（実行プログラム）
人工知能分野では、Pythonをベースとする多様なライブラリが公開されています。ここでもそれを用いたソースコードを示しますが、かなり手抜き（？）をしています。関心のある人はこちらを参照してください。
入力データ
ここでは特性を x1 とx2 の二つとし、それを配列として x とします。ラベルを y とします。画像認識では x が画像ファイルありはその画素配列になります。
教師あり学習では、x のデータと y のデータを、次の二つに分けます。ここでは事前に二分していますが、厳格にはランダムで分けます。
- 学習用データ（x_trainとy_train)
このデータを用いてモデルを作成します。ここでは５０組ですが、実務では数千・数万組になります。 - 評価用データ（x_testとy_test）
学習用データで作成したモデルにこのデータを入力して、精度（正答率）を評価します。ここでは１０個ですが、実務では数百・数千組になります。
学習用データ 評価用データ
(train) (test)
x1 x2 y x1 x2 y
1 2.65 2.21 1 2.28 2.41 1
2 1.79 2.60 1 1.87 2.40 1
3 -1.95 -2.97 0 -2.97 -2.11 0
: : : : : : :
9 -2.58 -2.06 0 -2.33 -3.66 0
10 2.21 1.32 1 2.28 2.88 1
11 -1.05 -0.86 0
12 -1.96 -2.93 0
: : : :
48 2.76 2.92 1
49 -2.20 -1.59 0
50 3.01 -1.03 1
モデルの設計
ニューラルネットワークの設計
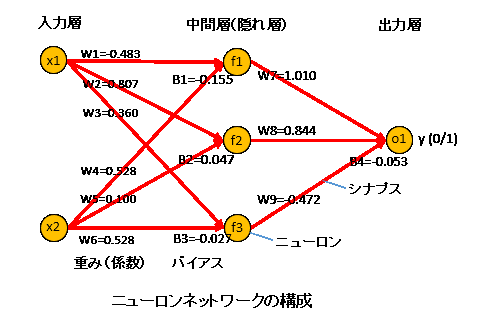
ここでは、非常にシンプルなモデルにしました。
import tensorflow as tf
model = tf.keras.models.Sequential([
tf.keras.layers.Dense(
# 入力層
input_shape=(2,), # 入力の形状とニューロン数
# 隠れ層
units=3, # ニューロンの数
activation='relu'), # 活性化関数
tf.keras.layers.Dense( # 出力層
units=1,
activation='relu'),
])
- tensorflow
Pythonをベースとするニューラルネットワーク分野のパッケージです。as ft とは、このパッケージの機能を使うときは、ft.… のように記述することを示しています。 - tf.keras
keras もPythonのパッケージですが、tf.kerasはtensorflow内でkerasのような記述ができる機能です。 - tf.keras.models.Sequential
Sequential とはニューラルネットワークのニューロン間の全てがシナプスで結ばれるタイプです。最も基本的なタイプです。 - layers.Dense
layerとは層のことです。Denseとは、層のタイプを指定したものです。
重さ、活性化関数
人間の脳と同じく、ニューロンは前の層からの信号を受けて、後の層に信号を伝播します。入力信号の強さにより、出力信号の強さが変わります。
上図の中間層 f1 を例にすれば、入力層 x1 と x2 から、
f1 = w1*x1 + w2*x2 + b1
の強さの信号を受けます。w1, w2, bを重さ、バイアスといいます。
ニューロン f1 は、この信号が強ければ、反応（発火）して、次の層に信号を送りますが、弱い信号のときは無視します。また、入力信号が強すぎるときは弱めた信号を送ります。それを活性化関数（activation）といいます。
活性化関数には幾つかのタイプがありますが、代表的なものにシグモイド関数があります。relu はtf.kerasが標準としている活性化関数の一つで、信号がプラスならそのまま受け取り、０あるいはマイナスならば無視するという最も単純な関数です。これを考慮すると、上の式は、
fi = relu(w1*x1 + w2*x2 + b1)
となります。
学習方法の設計
学習とは、x_train（x1,x2の組）と y_train（正解）のデータから、最適になるようにシステムがw1～w9, b1～b4の値を決定するプロセスのことをいいます。
学習方法の設計とは、何を最適にするのか、その最適化の方法は何かを指定することです。
教師が与えた「正解値」とモデルによる出力された「予測値」とのズレの大きさを「損失(loss)」といいます。そのズレの評価関数を損失関数（Loss function）あるいは誤差関数（Error function）といいます。通常は平均二乗誤差（MSE：Mean Squared Error）が用いられます。
最適化とは、損失関数を最小にするためのニューロンの重さを探すことだともいえます。
model.compile(
optimizer=tf.keras.optimizers.SGD(learning_rate=0.03),
loss='mean_squared_error',
metrics=['accuracy'])
- metrics（評価尺度）
ここではaccuracy（正解率）にしています。 - loss（損失）
正解率そのものを直接に最大化することはできません。その代わりに損失という値を設定して、それを最小化する方法をとえいます。ここではmean_squared_error（計算値とy_test値の差の二乗和の平均）を損失としています。最小二乗法での誤差分散の最小化と同じようなことです。 - optimizer
最適計算方法です。最適計算は複雑な非線形問題になります。SGD とは tf.keras の持つ最適計算方法の一つで、確率的勾配降下法という手法です。 - learning_rate（学習率）
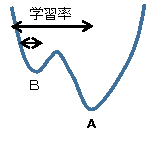数値計算で曲線の最大値や最小値を求めるには、範囲と刻み幅（dx）を与えますが、その刻み幅に相当するものです。
これが小さすぎると局部最小値（Ｂ）にとどまり全体最小値（Ａ）に到達できないことがあります。また、大きすぎるとその範囲内での真の最小値にたどりつけません。 - model.compile
これらのパラメタを解釈して、処理プログラムを作成する機能です。
学習と学習結果
設計したモデルに学習用データ（x_trainとy_train）を入力して実際に計算します。
hist = model.fit(
x=x_train, # 学習用データ
y=y_train, # 学習用ラベル
validation_split=0.2, # 精度検証用の割合：20％
batch_size=10, # バッチサイズ
epochs=15, # エポック数
verbose=1) # 実行状況表示
- 学習用データのうち、後方のvalidation_splitで指定した組数（ここでは 0.2*50=10組）を精度検証用データとします。それをここでは x_val, y_val ということにします。これは評価用データ（x_test. y_test）とは異なります。
- 残された学習用データを１回で全部使うのではありません。batch-size という部分に分け（システムが選択します）たデータを用いて、学習方法の設計で示した方法により、その小データに最適な重み付けを行います。
- その重み付けによって x_val, y_val の一致度を調べます。batch-sizeのデータは毎回変わるのに、 x_val, y_val は同じデータであることに留意してください。このサイクルをepochといいます。
- 次回のepochでは、次のbatch-sizeのデータを用いて、重みの変更をします。
- このようにして、epochが進む間に損失（loss）は減少し、正解率（accuracy）は１００％（＝１）に近づくでしょう。
評価用データ 精度検証用データ
損失 正解率 損失 正解率
Epoch loss accuracy val_loss val_accuracy
1 0.1233 0.9250 0.1594 0.8000
2 0.0940 0.9500 0.1216 0.9000
3 0.0645 0.9750 0.0777 1.0000
4 0.0635 0.9500 0.0938 1.0000
5 0.0557 0.9500 0.0735 1.0000
10 0.0441 0.9750 0.0732 1.0000
15 0.0391 0.9750 0.0667 1.0000
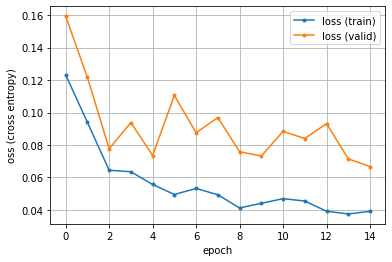
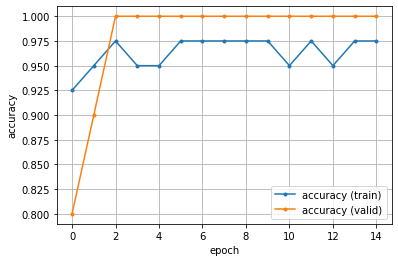
グラフに描く機能もあり、それを使えば下のようになります。未だ損失が高いですが、正解率はかなり高くなっています。
（注）過学習
この例では（幸運にも？）訓練用データと精度検証用データが、ほぼ同じような傾向になっています。
ところが、場合によっては、精度検証用データの損失の結果が、次第に増加したり大きく変動することがあります。
単純にいえば、モデルが過剰に精緻になり、新しい訓練用データ（バッチデータ）により、重箱の隅をほじくる状態になるのです。
そのため、パラメタの変化が激しくなり、いつも同じの精度検証用データでは、かえって損失が増大してしまうのです。
そのような状態が起きたときは、次のような手段が効果的です。
訓練用データを増やしバッチデータを大にする。
中間層の段数やニューロンの個数を減らす。
重みの小さいシナプスの線を削除（ドロップアウト）する。
活性化関数を工夫する。
重みの分析
学習後の「重み」を表示する機能もあります。
model.get_weights()
model.get_weights()[0] # 入力層→中間層（係数）
[[-0.4839(w1) 0.8074(w2) 0.3604(w3)]
[ 0.5285(w4) 0.1004(w5) 0.5286(w6)]]
model.get_weights()[1] # （バイアス）
[-0.1556(b1) 0.0473(b2) -0.0274(b3)]
model.get_weights()[2] # 隠れ層→出力層（係数）
[[ 1.0100(w7)]
[ 0.8447(w8)]
[-0.4727(w9)]]
model.get_weights()[3] # （バイアス）
[-0.0536(b4)]
この値と「評価用データによる評価」の結果との分析は後述します。
評価用データによる評価
ここまでで学習用データによるモデルが完成しました（不満足な結果ですが、とりあえず、これでよしとします）。
このモデルの正答率が安定しているか否かを評価するために、このモデルに評価用データ（x_test. y_test）を入力して結果を調べます。
x_pred = model.predict(x_test)
print(x_pred) # 出力層の入力信号
y_pred = np.where(x_pred > 0.5, 1, 0)
print(y_pred) # 分類
- model.predict(x_test)
predict とは予測のことですが、これで上のモデルに x_test を与えたときの結果（出力層が得る信号の値）が計算されます。 - np.where(x_pred > 0.5, 1, 0)
y_test が０／１の値ですので、やや強引（論理性に欠ける？）ですが、y_pred を四捨五入しました。
y_pred と y_test を比較すると完全に一致しました。これなら使えるでしょう。
実行結果 事前設定値
y_pred y_pred y_test
1 0.7830 1 1
2 0.7700 1 1
3 0.1143 0 0
4 0. 0 0
5 0.9564 1 1
6 0.6628 1 1
7 0.2339 0 0
8 0.8895 1 1
9 0. 0 0
10 0.8876 1 1
score = model.evaluate(x_test, y_test)
print('損失:', score[0]) # 損失
print('正解率:', score[1]) # 正解率
非常に簡素な評価関数です。意味は自明でしょう。
損失: 0.0308
正解率: 1.0
新規データの区分
新規データの x1, y1 を与えて、その区分を知るのは簡単です。データを y_test と同じ形式で記述して、model.predict を使えばよいのです。
x_new = np.array([
[ 2.28, 2.41],
[ 1.87, 2.40]
])
x_new_pred = model.predict(x_new)
[[0.7830935 ]
[0.77001023]]
重みとの関係
先に算出した w1～w9, b1～b4 から、x_pred. y_pred を算出できるのではないかと、評価用データの先頭５組について試しました。
表中の * は、入力信号が発火点０以下だったので、出力信号を出さない（０にする）という印です。
y_test（ア）と計算結果の y_pred（シ）は一致したのでしが、出力層入力信号の計算値（コ）と y_pred は、傾向は似ているものの数値としては一致していません。
おそらく、活性化関数が私が理解したよりも複雑なのではないかと思います。
いずれにせよ、現実モデルではシナプスの数が非常に大きく、重さを用いた数式を作成して用いるのは現実的ではないでしょう。それを作成するまでもなく、model.predict だけで計算できるのですから。
1 2 3 4 5
ア：y_test 1 1 0 0 1
イ：入力層x1 2.28 1.87 -2.97 -2.33 2.28
ウ：入力層x2 2.41 2.40 -2.11 -3.66 2.88
エ：ｆ１入力 0.0148 0.2079 0.1663 -0.9626 0.2632
オ：ｆ１出力 0.0148 0.2079 0.1663 0.* 0.2632
カ：ｆ２入力 2.1303 1.7983 -2.5628 -2.2016 2.1775
キ：ｆ２出力 2.1303 1.7983 0.* 0.* 2.1775
ク：ｆ３入力 2.0683 1.9153 -2.2133 -2.8020 2.3168
ケ：ｆ３出力 2.1303 1.7983 0.* 0.* 2.1775
コ：出力層 0.7537 0.8253 0.1143 -0.0536 1.0222
サ：x_pred 0.7830 0.7700 0.1143 0. 0.9564
シ：y_pred 1 1 0 0 1