Ｗｅｂ教材一覧＞ 統計・確率

確率分布

キーワード

確率分布、ベルヌーイ試行、二項分布、負の二項分布、幾何分布、超幾何分布、ポアソン分布、指数分布

確率分布

数枚の硬貨を投げたとき表が何回でるか、多数の部品からなる装置で、１日に故障が何回発生するかといったような回数は、確率で計算できます。このような回数を変数と考えたとき、それを確率変数といいます。すなわち、確率変数とはどのような値を取るかが確率で決まっている変数です。

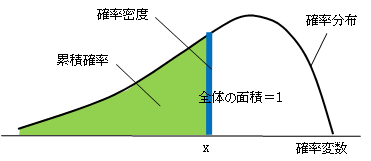
確率分布とは確率変数がどのような値になるかという分布を示したものです。
　そして、その分布は確率の理論により計算できますが、
　　・確率密度Ｐ(x)：確率変数の値がｘであるときの確率
　　・累積確率Ｐ(≦x)：確率密度の０～ｘまでの累積
が多く用いられます。
　確率分布の特徴は、確率変数がとるすべての範囲での累積確率が１になることです。逆にいえば、そのような分布を確率分布というのです。

ここでは、基本的な確率分布について学習します。

複雑な計算を伴うので、Ｅｘｃｅｌの関数を用いるのが便利です。そのテンプレートが、こちらにあります。ダウンロードしてください。

二項分布

ポアソン分布と指数分布

理解度チェック

第１問

  1. 確率分布を図示したとき、確率変数がとれる全範囲での確率分布の面積は１になる。 ☆
    ○
  2. 硬貨をなげるときの結果は裏と表の２つの値になるので二値性であるが、サイコロの場合は６つの場合があるので二値性がない。 ☆
    ×　二値性とは、ある事象が起こるか起こらないかの２つ
  3. １つの硬貨をｎ回投げたときに、表がｘ回でる確率を求めるには二項分布が用いられるが、ｎ個の硬貨を同時に投げたときに、表がｘ回である確率を求めるには二項分布は利用できない。 ☆
    ×　どちらも同じ試行。二項分布が用いられる
  4. ある事象が起こる確率がｐのとき、ｎ回試行したときに、その事象がはじめて起こる確率は、指数分布になる。 ☆
    ×　幾何分布になる
  5. 発生確率×平均発生回数が大のとき、二項分布は正規分布で近似できる。 ☆
    ×　発生確率×試行回数
  6. 「袋の中に赤玉が５つ、白玉が４つ入っている。玉を４つ取り出したとき、赤玉が３個と白玉が１つである確率を求めよ。」という問題には、超幾何分布が用いられる。 ☆
    ○
  7. １日に発生する交通事故の発生回数は、二項分布に従う。 ☆
    ×　ポアソン分布
  8. ポアソン分布は、平均発生回数とその分散がパラメータとし、発生回数を変数とする分布である。 ☆
    ×　パラメータは平均発生回数だけ
  9. ポアソン分布では、ファミリレストランのように、客が連れだってくるような場合に、単位時間で客が何人来るかの確率を計算するのに適した分布である。 ☆
    ×　ポアソン分布は稀少性を前提
  10. 　発生回数がポアソン分布に従うとき、発生間隔は指数分布になる。 ☆
    ○
  11. ５つのサイコロを投げたとき、１の目が３つ以上でる確率を求めよ。 ☆

    二項分布を用いる。
    Ｐ(３)＝5Ｃ3(1/6)3(5/6)2＝0.03215
    Ｐ(４)＝5Ｃ4(1/6)4(5/6)1＝0.003215
    Ｐ(５)＝5Ｃ5(1/6)5(5/6)0＝0.000129
    Ｐ(≧３)＝0.03215＋0.003215＋0.000129＝０.０３５５

  12. ある製品の２０％が不良品だという。製品を１つずつ取り出して検査し、不良品が見つかったら終了する。検査が５回までに終了する確率を求めよ。 ☆

    幾何分布を用いる。
    Ｐ(1)＝0.80×0.2＝0.2
    Ｐ(2)＝0.81×0.2＝0.16
    Ｐ(3)＝0.82×0.2＝0.128
    Ｐ(4)＝0.83×0.2＝0.1024
    Ｐ(5)＝0.84×0.2＝0.08192
    　　　　　　　　　-------
    　　　　　　　　　0.67232

  13. 袋の中に赤玉が５つ、白玉が４つ入っている。玉を４つ取り出したとき、赤玉が３個と白玉が１つである確率を求めよ。 ☆

    超幾何分布を用いる。
    　　　　5Ｃ3×4Ｃ1　１０×４
    Ｐ(x)＝─────＝────＝０.３１７
    　　　　　9Ｃ4　　　１２６

  14. ある工場では、多数の機械があり、平均すると１日３台の機械が故障する。１日５台以上故障する確率を求めよ。 ☆

    ポアソン分布を用いる。
    λ＝３であるから、ｅ－λ＝ｅ-3＝0.049787
    Ｐ(0)＝30／0!×ｅ-3＝ 1/ 1×0.0498＝0.498
    Ｐ(1)＝31／1!×ｅ-3＝ 3/ 1×0.0498＝0.149
    Ｐ(2)＝32／2!×ｅ-3＝ 9/ 2×0.0498＝0.224
    Ｐ(3)＝33／3!×ｅ-3＝27/ 6×0.0498＝0.224
    Ｐ(4)＝34／4!×ｅ-3＝81/24×0.0498＝0.168
    　　　　　　　　　　　　　　　　　------
    　　　　　　　　　　　　　Ｐ(≦4)＝0.815
    （Ｐ(≦4)はPOISSON(4,3,TRUE)から計算できる。）
    従って、Ｐ(≧5)＝１－０.８１５＝０.１８５

  15. ある店では、１時間に平均５人の客が来る（平均到着間隔＝１２分）。９５％の確率で到着間隔は何分以下だといえるか。 ☆

    指数分布の累積確率の公式を用いる。
    λ＝５[人/時間]であるから、
    　　Ｐ(≦ｔ)＝１－ｅ－λｔ≧０.９５
    となるｔを求めればよい。
    ｔ≧－(loge0.05)/5＝2.99573/5＝0.599[時間]＝３６[分]

「確率・統計」の目次