適合度検定とは、次のような検定を行うことです。
- サイコロ
正しいサイコロならば、ある目が出る確率は、すべて1/6のはずです。実際に多数回サイコロを振ってみて、それぞれの目が出た頻度から、すべての目が出る確率が1/6といえるかどうかを検定します。 - 曲線のあてはめ
多数の点をプロットしたところ、これから数式があてはまると予想しました。その数式による計算値と測定値から、その数式にあてはまるかどうかを検定します。
このような適合度検定の方法のうち、最もポピュラーなのが、χ2による検定です。
理論
帰無仮説 H0:正しいサイコロである。数式があてはまる。
対立仮説 H1:サイコロの出る目に偏りがある。数式にあてはまるとはいえない。
標本の個数をnとし、標本iの測定値をOi、理論値をEiとすると、
(Oi-Ei)2
χ*2 = Σ──────
Ei
は、自由度φ(=n-1)(注1)のχ2分布に従う。
χ*2が、自由度φ、有意確率αのχ2の値よりも
大ならば、帰無仮説H0は棄却され(サイコロが正しくない、数式にあてはまらない)、
小ならば、棄却されない(正しいサイコロである、数式にあてはなる)ことになる(注2)。
- 注1:この場合はサイコロの目は一様分布だとしてφ=n-1としたが、分布により自由度は次のようになる。
一様分布のとき、φ=n-1
二項分布、ポアソン分布のとき、φ=n-2
正規分布のとき、φ=n-3 - このような検定方法は、n≦5 のときに用いるのは不適切で、工夫が必要だといわれている(省略)。
数値例(サイコロの例)
サイコロを60回振って次の度数表を得ました。
目の数 i 1 2 3 4 5 6 合計
観測度数 Oi 12 7 13 14 8 6 60
期待度数 Ei 10 10 10 10 10 10 60
このサイコロはイカサマなのではないか? という問題です。
(12-10)2 (7-10)2 (13-10)2 (14-10)2 (8-10)2 (6-10)2
χ*2 = ────+────+────+────+────+──── = 5.8
10 10 10 10 10 10
χ2分布表(上側確率ポイント)から、自由度=6-1=5の確率α=0.05のχ2値は、11.07です。
5.8<11.07なので、帰無仮説は棄却されません。すなわち、正しいサイコロでも、この程度の偏りが起こることはあるので、イカサマだと決めつけることはできないという結論になります(当然ながら、正しいサイコロだと証明したことにはなりません)。
計算プログラム
曲線のあてはめ
n個の点 (x,y) が、与えられた曲線(論理式)に合致するといえるかどうかの検定に、χ2検定を用いることがあります。測定した値と論理式との関係(差の分布)が曖昧ですので、統計学上は厳密性を欠くのですが、簡単な計算で検定できますので、よく用いられています。
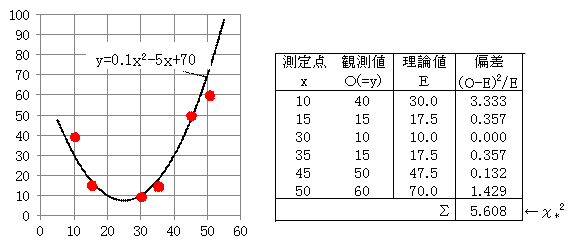
左のグラフで、赤点の散布図を眺めて、目視や最小二乗法による近似式として、あるいは何らかの理論式として、y=0.1x2-5x+70という式が与えられたとします。
それを上記の公式に当てはめ、右表の計算をすると、χ*2= 5.6078 が得られました。
測定点は6なので自由度=6-1=5の確率α=0.95のχ2値は、1.145です。5.6078>1.145 なので、測定点の組 (x,y) は、95%の信頼性では、この式に当てはまるとはいえないと判定します。
サイコロの例ではα=0.05を用い、曲線あてはめではα=0.95を用いました。
前者では、違いがあるかを検定したのに対して、後者では違いがないかを検定しているからです。