双対問題の概念
次のような問題が与えられていたとします。
目的関数
v1x1+v2x2+・・・+vnxn → 最大
制約条件
a11x1+a12x2+・・・+a1nxn ≦ b1
a21x1+a22x2+・・・+a2nxn ≦ b2
・・・・・・・・・・・
am1x1+am2x2+・・・+amnxn ≦ bm
x1,x1,・・・,xn ≧ 0
この問題を、m個の変数u1,u1,・・・,um を考えることにりり、次のように変形します。
・制約式の右辺 b を、目的関数の係数にする。
・目的関数の係数 v を、制約式の右辺にする。
・制約式の不等号の向きを反対にする。
・制約式の係数 aij の行と列をとりかえて、 aji を係数とする。
・最大値問題を最小問題にする。
すなわち、次の式になります。
目的関数
b1u1+b2u2+・・・+bmum → 最小
制約条件
a11u1+a21u2+・・・+am1um ≧ v1
a12u1+a22u2+・・・+am2un ≧ v2
・・・・・・・・・・・
a1nu1+a2nu2+・・・+anmun ≧ vm
u1,u1,・・・,un ≧ 0
このように変形した問題を双対問題(双対-そうつい-Dual)といいます。これは元の問題を裏返しにした表現であり、元の問題は新しい問題の双対問題であるともいえます。
元の問題と双対問題の解には、次の対応があります。
・最適値はどちらも同じになる。
・双対問題の最適解 uopti は、元の問題の制約式 bi のシャドウ・プライスになる。
(uopti が0ならば、bi には余裕がある。)
・双対問題の vj のシャドウ・プライスは、元の問題の制約式 xi の最適解になる。
元の問題でのシャドウ・プライスとは、「その制約が少し変化したら、最適値がどれだけ変化するか」を示しています。そのため、最大化を図るということは、改善の余地を最小にすること、すなわちシャドウ・プライスを最小にするだといえます。
数値例
非常に簡単な数値例により、具体的に説明します。
●元の問題
目的関数
6x1+5x2 → 最大
制約条件
2x1+1x2 ≦ 5
3x1+4x2 ≦ 10
●双対問題
目的関数
5u1+10u2 → 最小
制約条件
2u1+3u2 ≧ 6
1u1+4u2 ≧ 5
双対問題の定式化では、次の表を用いると便利です。
元の問題 双対問題
変数1 変数2 制約値 制約式1 制約式2 制約値
目的関数 6 5 → 最小 制約値 6 5 最大
∧ ∧ ↑
制約式1 2 1 ≦ 5 変数1 2 1 5
制約式2 3 4 ≦ 10 変数2 3 4 10
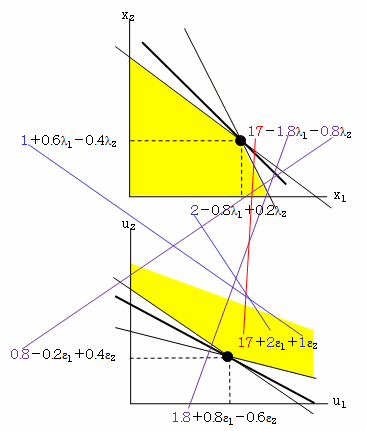
元の問題の制約式を等号にしたときの点、x1=2,x2=1 が最適値であることは簡単にわかります。ここで、制約式を等号にするために、非負の変数λを導入します。
2x1+1x2 + λ1 = 5
3x1+4x2 + λ2 = 10
これを解くと、
x1 = 2-0.8λ1+0.2λ2
x2 = 1+0.6λ1-0.4λ2
となり、目的関数は
6x1+5x2 = 17-1.8λ1-0.8λ2
となります。
すなわち、制約式1のシャドウ・プライスは-1.8、制約式2のシャドウ・プライスは-0.8になります。
同様に双対問題で、変数εを導入すれば、
2u1+3u2 - ε1 = 6
1u1+4u2 - ε2 = 5
u1 = 1.8+0.8ε1-0.6ε2
u2 = 0.8-0.2ε1+0.4ε2
5u1+10u2 = 17+2ε1+1ε2
になります。
これらから、前述した元の問題と双対問題での変数の最適値と制約式のシャドウ・プライスの関係が成立していることがわかります。
ここで、λとεについて考えてみましょう。
元の問題での制約式1を、
2x1+1x2 ≦ 5 - λ1
とすれば、双対問題での目的関数は、
(5-λ1)u1+10u2 → 最小
となります。
ここで、λ1 を1単位変化させることは、制約式1の制約を1だけ変化させることです。そのときに目的関数の値が u1 だけ変化するということは、u1 が制約式1のシャドウ・プライスであることを示しています。
また、双対問題の制約式1を
2u1+3u2 ≧ 6+ε1
とすると、元の問題の目的関数は、
(6+ε1)x1+52x2 → 最大
となります。
すなわち、ε1は、x1の価値の増大分だと解釈できます。そして、制約式1の左辺は「x1は、少なくとも6以上の
価値をもたなければならない」という意味だと解釈できます。双対問題の制約式は、変数xを使うことの価値、変数xをいくつにすればよいかに関する条件なのですから、そのシャドウ・プライスが変数xの最適値を示すことになるのです。