破産確率とは
Aの当初の資金をn、Aが勝つ確率(勝率)をpとします。Aが勝てばa円をBから貰い、負ければb円をBに払うというゲームを行います。このとき、k=a/bのことを損益率といいます。
そして、Aの所持金が
(幸運にも)m円になる・・・このmを目標金額という
(不幸にも)0円になる・・・破産するという
まで、勝負を続けるとします。
このとき、Aがm円を得る以前に破産する確率を破産確率といい、Q(n) で表します。
この破産確率を求めるのが、ここでの目的です。
p=0.5、a=b=1ならば、統計的には損得がないので、当初の資金nには無関係のように思われます。
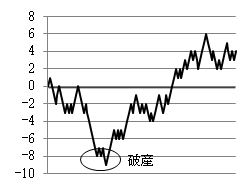
ところが、実際には勝ち続けたり負け続けたりすることが多くあります。右のグラフは、乱数を用いて勝負を判定させ、上のゲームを、100回行ったときの、Aの持金の増減を示したものです(このような動きをランダムウォーク(酔歩)といいます)。
Aが、豊富な資金をもっているならば、何度も行っているうちには、利益を得る機会は必ずあるので破産しないでしょう。ところが、資金が少ないとき(例えば8円しかもっていないときは)、このグラフのように初期に負けが続くと、破産してしまいます。
このように、公平な賭けでも資金が少ないと破産する確率が大きくなるのです。
損益率が同じときの定式化
まず、損益率が同じ場合でa=b=1のときを対象にします。
ある時点で所持金nを持ち破産していない確率は、1-Q(n) です。
これは、前回に
勝ったことにより、n+1円を持ち破産していない確率: p (1-Q(n+1))
負けたことにより、n-1円になったが破産していない確率:(1-p) (1-Q(n-1))
から生じているのですから、
1-Q(n) = p (1-Q(n+1)) + (1-p) (1-Q(n-1))
すなわち、
Q(n) = p Q(n+1) + (1-p)Q(n-1) ・・・★漸化式
の関係があります。
この漸化式の特性方程式は、
x=px2+(1-p) ・・・★特性方程式
ですから、x=1、x=(1-p)/p(これをrとします)の根を持ちます。
そして、Aの所持金が0になるか、目的金額であるm円になったときに、この賭けを終了するので、
n=0:Aは既に破産しているので、Q(0)=1
n=m:Aは既に目標金額を得ているので、Q(m)=0
になります。
この結果、次の公式が得られます。
Q(n)=1-n/m (p=1/2のとき)
・・・★基本公式
rn-rm 1-p
Q(n)=──── (r=───≠1) (p≠1/2のとき)
1-rm p
派生公式
●Bの資金がAと同じとき
m=2nですから、
r=1(p=0.5)のとき
Q(n)=1-n/2n=0.5
r≠1(p≠0.5)のとき
rn-r2n rn(1-rn) rn
Q(n)=────── = ────────── = ────
1-r2n (1+rn)(1-rn) 1+rn
●Bの資金が非常に大きいとき
r=1(p=0.5)のとき
Q(n)=1-n/m=1
r>1(p<0.5)のとき
rm→∞ になるので、
rn-rm rn-rm rn
Q(n)=────── = ───── = 1- ── = 1
-rn-m → 1
1-rm -rm rm
r<1(p>0.5)のとき
rm→0 になるので、
rn-rm
Q(n)=───── = rn-rm → rn
1-rm
数値例と分析(参照:「破産確率のシミュレーション」)
●例1 対等なとき
AもBも当初の資金は100円、賭金は1円、Aの勝率が1/2のとき。すなわち、AとBが同等であり、一方が破産するまで行うものとします。
Aについていえば、n=100、m=200、p=0.5になります。
「Bの資金がAと同じとき」の「p=0.5」より、
Q(n)=0.5
となります。これは当然でしょう。
●例2 資金豊富な相手
他の条件は例1と同じで、Bの当初資金が900円、すなわちm=1,000としたとき。
Q(n)=1-n/m=1-100/1000=0.9
となります。すなわち、同等な賭けをしているのに、90%の確率で破産してしまうのです。相手が無限の資金を持っていれば、破産確率は100%になり、必ず破産することになります。
[教訓]資金が豊富な相手と賭けをするときは、同等な条件でも破産する確率が高くなる。
これは、冒頭のランダムウォークの説明からも納得できましょう。
●例3 勝率がわずか不利のとき
他の条件は例1と同じで、勝率p=0.49としたとき。
「Bの資金がAと同じとき」「p≠0.5」ですから、
rn
Q(n)=────
1+rn
を用います。
この例では、p=0.49ですから、r=0.51/0.49、(0.51/0.49)100=54.6です。
54.6
Q(n)=────── = 0.982
1+54.6
となります。勝率が50%から49%に下がっただけなのに、破産確率は50%から98.2%へと急激に増加するのです。
[教訓]勝率がわずかでも不利な賭けを続けると、破産確率は非常に大きくなる。
●例4 勝率が不利で賭金を2倍にしたとき
例3で、賭金を1円ではなく2円にしたらどうなるでしょうか。
この場合は、n=50、m=100としたことと同じです。
(0.51/0.49)50=7.39ですので、Q(n)=0.881 になります。すなわち、賭金を2倍にしたら、破産確率は小さくなるのです。
極端な例として、賭金が100円で1回勝負をするならば、Aの破産確率は51%です。
[教訓]勝率が不利な場合は、1回勝負に出るのが最も安全である。
逆に、勝率が有利ならば、賭金を小さくせよ。
損益率が異なるとき
損益率k(=a/b)≠1のとき、すなわち、勝ったときの金額aと負けたときの金額bが異なるときの破産確率を考えます。
ここでは、相手Bは、カジノの胴元や金融市場のように、非常に大きい資金をもつ相手であるとします。
また、p≦b/(a + b) だと、毎回損をするので、必ず破産してしまいます。それで、p>b/(a + b)のときだけを扱います。
k=1(a=b=1)のときの定義公式を導く漸化式は、
Q(n)=pQ(n+1)+(1-p)Q(n-1)
となります。このときの 特性方程式は、
x=px2+(1-p)
となります。x=1とr (0<r<1)の二つの解がありますが、x=rを採用します。
これにより、定義公式および「Bの資金が非常に大きいとき」の「r<1(p>0.5)」での派生公式、
Q(n)=rn
が得られたのです。さらに例4の説明から、賭金をb円とするならば、
Q(n)=rn/b
であることを知りました。
k≠1の場合は、上の関係を発展させて、
漸化式: Q(n)=pQ(n+k)+(1-p)Q(n-1)
になるので、
特性方程式: x=pxk+1+(1-p)
が得られます。
この方程式の0<x<1での解をrとすると、
Q(n)=xn/b
となることが類推できます。
数値例と分析(参照:「破産確率のシミュレーション」)
●例5 k=1での確認
資金n=10、勝率p=0.6、損益率k=1(a=b=1)のときの破産確率はどうなるでしょうか。
まず、「損益率が同じ」「Bの資金が非常に大きいとき」「r<1(p>0.5)」の式、
Q(n)=rn
で計算してみます。r=0.4/0.6=1.5ですから、
Q(n)=rn=1.510=0.0173
すなわち、17.3%になります。
次に、「損益率が異なるとき」の手順で行ってみましょう。
特性方程式
x=pxk+1+(1-p)
は、次の式になります。
x=0.6x2+0.4
0<x<1での解は、x=0.667になります。
このxと、n=10、b=1を
Q(n)=xn/b
に代入すれば、0.66710=0.0173
となり、両者は一致します。
●例6 k≠1の場合
資金n=10、勝率p=60%、損益率k=2(a=1、b=2)の場合はどうなるでしょうか。
特性方程式、
x=0.6x3+0.4
の根は、x=0.457になります。
Q(n)=xn/b=0.4575=0.0199
すなわち、約2%(ほとんど破産しない)になります。
(こんなに条件のよい賭けならば当然でしょう)
●例7 賭金の影響
例6で、損益率k=2なのですが、a=2、b=4としたらどうなるでしょうか。
特性方程式は同じですので、x=0.457は変わりませんが、n/b=10/4=2.5になります。
Q(n)=0.4572.5=0.156 → 15.6%
すなわち、かなり条件のよい賭けでも、賭金が大きいと破産確率が大きくなることがわかります。
ここでも、例3の教訓「勝率が有利ならば、賭金を小さくせよ。」が生きています。
破産確率表
ここで紹介した破産確率は、(公営を除き賭博は禁止されていますので)最も活用されているのは、株取引や先物取引などの分野です。金融工学の基本にもなっており、高度な理論や統計学的なデータ活用が行われています。
次の表は、どのような前提でどのように定式化したのか私はしらないのですが、バルサラの破産確率表として、株取引や先物取引などではポピュラーなもの(らしい)です。
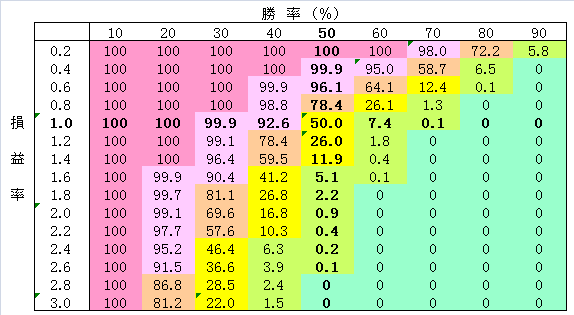
私はこの分野には疎いのですが、一般に破産確率が1%以内であることが健全だといわれているそうです。
例えば、100万円の投資をして、200万円になる(損益率=2)ような投資があるとき、それが当たる確率(勝率)が60%以上ならば、破産確率は0に近いので、安心して投資してもよいが、50%以下のときは、慎重になるべきだと読むことができます。