問題の理解
問題
1単位生産した販売すると1億円の利益がある製品を生産する工場建設計画があります。対象期間を前半・後半に分けて次の3つの案があります。
① 当初から生産能力300単位の工場(大規模)を建設する。建設費用100億円。
② 当初は100単位の規模(小規模)にして,増強しない。建設費用50億円。
③ 当初は100単位の規模(小規模)にして,後半で増強する。追加建設費用80億円。
前半・後半の需要は次のように確率的に予測されています。
確率 需要予測 前半:好況 0.4 130 不況 0.6 80 後半:好況 0.7 200 不況 0.3 100
期待利益を最大にするために,当初に大規模にするか小規模にするかを決定しなさい。
この問題は,「当初投資の決定→前半の景気→後半投資の決定→後半の景気」の順序で発生しており,意思決定と不確実事象が複数回繰り返される特徴があります。このような問題を多段階意思決定の問題といいます。
デシジョンツリーによる解法
多段階意思決定問題の解法の代表的なものにデシジョンツリーがあります。その手順を説明します。
デシジョンツリーの作成
上記の問題を下図のように図示します。横から見ると,最初の決定を根として枝分かれしているように見えますので,これをデシジョンツリー(決定木)といいます。意思決定を□,不確実事象を○で表します。
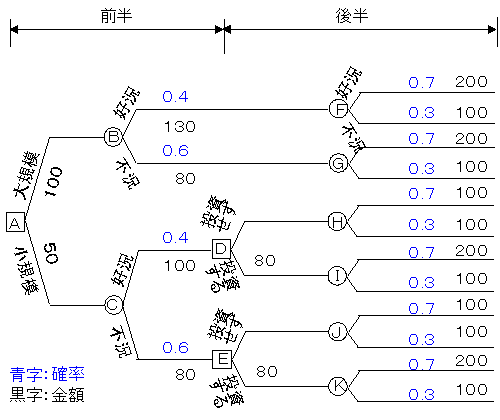
右から計算
このツリーから計算するには,右から計算することがポイントです。
○不確実事象の扱い
まず,Fの付近を取り上げます。Fで後半が好況の確率は0.7で,それが実現したときの利益は200億円ですから,その期待値は0.7×200=140億円になります。同様に,不況のときの期待値は30億円になります。それでF点直前での期待値は140+30=170億円になります。
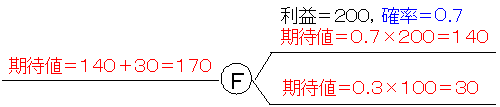
同様にGの直前での期待値も170億円になります。
Bの好況のときは,後半に170億円の期待利益があり,前半では130億円の利益があるのですから,全期を通して170+130=300億円の利益となります。その確率が0.4ですから,前半が好況のときの全期を通しての期待値は,0.4×300=120億円になります。同様に不況のときの期待値は,0.6×(170+80)=150億円となり,B点直前では120+150=270億円になります。
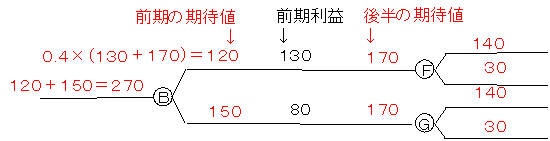
次にH点付近を取り上げます。Hのときは,小規模投資のままですので,需要が200単位あっても能力が100単位ですので利益は100億円,期待値は0.7×100=70億円になります。不況のときの期待値は0.3×100=30億円ですから,H点直前での期待値は70+30=100億円になります。同様にI点直前の期待値は170億円となります。
ここでDで「投資せず」のときは,費用はかからないのですから,H点直前の期待値100億円がそのまま「投資せず」の期待値になります。それに対して「投資する」ではI点直前の期待値は170億円ですが,追加投資費用が80億円ですから,「投資する」の期待値は170-80=90億円になります。
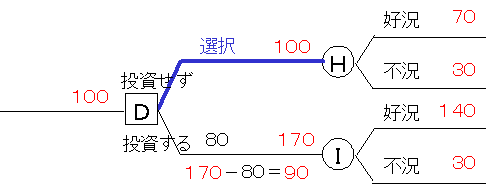
□意思決定の扱い
G点では,「投資せず」を選択すれば利益の期待値が100億円で,「投資する」を選択すれば90億円になります。当然,経営者は「投資せず」を選択します。
このように,意思決定点□では,そこから右に複数の線が出ているとき,期待値が最大であるものを選択し,その最大値が□の直前の期待値にになります。
それでD点直前の期待値は最大であった100億円になります。このとき,こちらを選択したことを記録するために,D-Hを太線にしておきます。
全体の計算
E点付近の計算は,D点付近の計算と同様に行うことができます。
- H直前の100億円になります。
- I直前の期待値は170億円になりますが投資額が80億円ですのでD直後の期待値は170-80=90億円になります。
- それで意思決定点Dでは「投資せず」になり,D点直前の期待値は100億円になります。
C点の前後では次のようになります。
- 好況のときは,後半(D直前)の期待値は100億円,前半は需要は130あるのに工場能力が100しかないので,前半の利益は100億円になります。それで全体では100+100=200億円になります。
- 好況になる確率は0.4なので,好況になるときの期待値は0.4×200=80億円になります。
- 不況のときは,0.6×(100+80)=108億円の期待値になります。
- それで,C点直前の期待値は80+108=188億円になります。
Aの直後を考えます。
大規模投資の期待値は,B直前の期待値270億円から投資費用の100億円を引いて170億円になります。
当初に小規模投資をするときは,C点直前の期待値188億円から投資費用の50億円を引いて150億円になります。
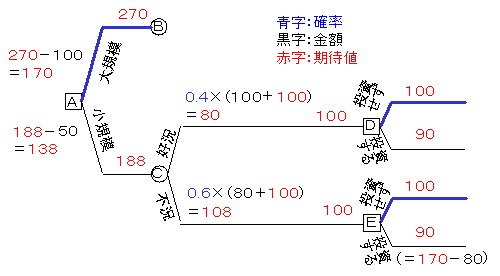
大規模の期待値170億円>小規模の期待値150億円 ですから,A点での意思決定では,大規模投資が有利となります。なお,A点で大規模にするのですから,D点やE点の意思決定は関係ないことになります。
調査費用の問題
同じような問題をもう一つやってみましょう。
生産設備の大規模計画と小規模計画があります。大規模計画では建設費用が100億円かかりますが,景気が好況ならば200億円,不況では100億円の利益が期待できます。小規模計画では,建設費用は50億円ですが好況でも不況でも100億円の利益になります。なお,経営者は経験やカンにより,好況になる確率を70%,不況になる確率を30%と見込んでいます(下左表)。
そのときの利益の期待値は,
好況のとき 不況のとき 建設費用 期待値
大規模:0.7×200+0.3×100-100 = 70 ←最大
小規模:0.7×100+0.3×100- 50 = 50
となるので,このときの期待値は70億円となります。
景気の動向を調査しようという意見がありました。経営者は調査をしても,好況と予報したときに当たる確率は90%になりますが,不況と予報したときに当たる確率が60%であると思っています(下右表)。調査にどれだけの費用をかけることが正当化されるでしょうか。
| 景気と収入 | 好況 | 不況 | 建設費用↓ 主観確率→ | 0.7 | 0.3 |
|---|---|---|---|
| 建設計画 | 大規模:100 | 200 | 100 |
| 小規模: 50 | 100 | 100 | |
| 実際の景気 | 好況 | 不況 | |
|---|---|---|---|
| 景気調査 の結果 |
好況 | 0.9 | 0.1 |
| 不況 | 0.4 | 0.6 | |
デシジョンツリーの作成
デシジョンツリーは下図のようになります。
調査した結果が好況となるか不況となるかは,調査をしなければわかりませんが,経営者は好況になる確率を70%と思っているのですから,その調査でも好況と報告する確率は70%であると考えるのが妥当でしょう。また,その調査報告を聞いてから建設規模を決めるのですが,報告が好調となっても,実際に好況である確率は90%であり,10%は不況の場合があります。
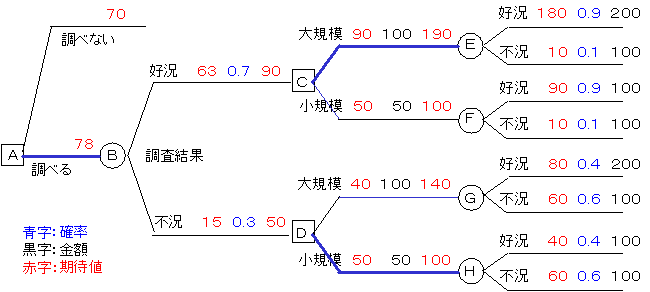
その結果は上図のようになり,調査をしないときの期待値は70億円で,調査をしたときの期待値は78億円になります。それで調査費用は8億円以下であればよいことになります。
簡単に説明をしておきます。
調査をしないとき
- 大規模投資をしたときは,利益の期待値は0.7×200+0.3×100=170億円で,建設費が100億円ですから,170-100=70億円の利益になります。
- 小規模投資のときは,0.7×100+0.3×100-50=50億円になります。
- それで「大規模投資をする」決定を行い,その期待値は70億円になります。
調査をするとき
E・F・G・Hの直前
- E点直後で好況のとき:調査結果が「好況」であるとき,本当に好況である確率は0.9ですから,好況になるときの期待値は0.9×200=180億円になります。
- 同様にE点直後で不況のときの期待値は,0.1×100=10億円になります。
- それで,E直前の期待値は180+10=190億円になります。
- 同様にして,F,G,H直前の期待値は上図のようになります。
C・D直前
- Cで大規模にしたときは,E直前の利益190億円を得るのに建設費用100億円なので,190-100=90億円になります。
- 同様に,小規模にしたときは,100-50=50億円。
- 従って,Cでは「大規模」にするので,C直前の期待値は90億円になります。
- 同様にDでは,「小規模」にするので,D直前の期待値は50億円。
B直前
- 調査結果はやらなければ不明ですが,経営者は0.7の確率で好況になると思っているのですから,調査結果が「好況」となる確率は0.7であると経営者は予想するでしょう。
- それで,「好況」の報告がきたときの期待値は0.7×90=63億円となり,「不況」の報告がきたときの確率は0.3×50=15億円になり,B直前の期待値は63+15=78億円になります。
詳細は省略しますが,このような考え方をベイズの理論といいます。主観確率と客観確率がうまく組み合わされていることが理解できるでしょう。