データ圧縮の概要
- データ圧縮(符号化)とは
- データ圧縮とは、元のデータのビット列(文字列)を、より小さなビット列に変換(符号化という)して、ファイル全体のビット数を小さくすることです。
例えば、「すもももももももものうち」というデータは12文字ありますが、「同じ文字が並ぶ場合は、その文字の後に並ぶ回数を数字で示す」という符号化規則を適用すると「すも8のうち」の6文字に圧縮されます。
そして、圧縮の効果を
圧縮率=圧縮後のビット数/圧縮前のビット数
で表します。
圧縮率を高めるには、元データが持つ次の3つの性質に着眼する必要があります。
冗長性:繰返し発生するビット列をまとめて符号化する
予測可能性:あるビット列の次にくるビット列の頻度により、割り付ける符号の長さを工夫する
不要性:圧縮後のデータが実用に耐える範囲で、元データの不要部分を削除する - 可逆圧縮と非可逆圧縮
- 圧縮された(符号化された)データから、元のデータを復元することを、復元、展開、伸張、解凍などといいます。
元のデータと全く同じ内容に復元できるように符号化することを可逆圧縮といいます。先の「すも8のうち」が可逆圧縮であることは明白でしょう。一般に文書やデータファイルなどのテキストデータは、可逆圧縮であることが求められます。 それに対して、画像や音声などのマルチメディアでは、少々音質や画質が悪くなっても高い圧縮率にすることが求められる場合があります。その場合には、必ずしも元のデータに復元できる必要はありません。そのような圧縮を非可逆圧縮といいます。 - 静的符号化と動的符号化
- 静的符号化とは、あらかじめ符号化の方法を定めておき、それに従って符号化する方法です。
最も単純なのは、文字列に対応する符号の対応表を辞書として用意しておき、該当する文字列が出現したら符号に置き換える方法です。商品コードなどのコードも、符号化の一つだといえます。しかし、これでは高い圧縮率が期待できませんし、汎用性がありません。一般的には、まず全データをスキャンして符号化の方法を作成して、次に符号化するという2つのステップで圧縮する方法がとられます。
それに対して動的符号化では、データを符号化しながら動的に符号化の方法を作成・更新していく方法です。
主な圧縮方法
どのようなデータについても高い圧縮率が得られるようにすること、圧縮処理を効率的に行えるようにすることを目的として、多様な圧縮法(符号化法)が研究されています。
可逆圧縮
静的符号化
シャノン・ファノ符号化
ハフマン符号化
算術符号化
動的符号化
連長符号化
動的ハフマン符号化
ユニバーサル符号化
非可逆圧縮
画像符号化 JPEG、GIFなど
音声符号化 MP3など
動画符号化 MPEGなど
ここでは、連長符号化とハフマン符号化について簡単に説明します。なお、マルチメディアで用いられる符号化に関しては別章で扱います。
連長符号化
- 基本的な考え方
- 連長符号化(RLE:Run Length Encoding、ランレングス法)は、前述の「すもももももももものうち→すも8のうち」のように、コードの冗長性(繰返し)を利用して圧縮します。
通常の文章データでは、このような方法では高い圧縮率が得られないどころか、かえってビット数が増大してしまうことがあります(売上ファイルなどのデータファイルでは、0が続くことが多く効果がある場合もあります)。それに対して画像データでは、画像を小さな点(画素)に分解し、その点を色の3原色の強さによりデジタル化しますが、ある範囲に同じ色が連続していることが多いので、この方法が適しています。WindowsのBMPファイルでの圧縮に用いられています。 - LZ符号化
- 連長符号化を発展させたものに、ユニバーサル符号化の一つであるLZ符号化があります。元データのビット列の組み合わせパターン(語句)の冗長性を利用して、元データを「ここからのデータは何文字前の何文字分と同じである」こと符号化することにより、連長符号化よりも高い圧縮率を実現できます。
- MH(Modified Huffman)
- MR(Modified Read)
- MMR(Modified Modified Read)
- いずれもファクシミリ用の圧縮方式で、モノクロのビットマップイメージだけに適用され、圧縮モード/非圧縮モードを指定できます。走査線のデータを符号化するときに、一つ前の走査線のデータとの差を検出して符号化します。
ハフマン符号
ハフマン符号はシャノン・ファノ符号を改良をしたに発展したもので、両者は非常に良く似ています。現在では、ハフマン符号が広く用いられていますので、ここでは、両者を含めてハフマン符号としています。
- 基本的な考え方
- ハフマン符号は、予測可能性を重視して可変長符号を用いた符号化です。頻繁に出てくる記号は短いビット数で符号化し、あまり出てこない記号は長いビット数で符号化することにより、全体としてデータを圧縮する手法です。
例えば、元データが
「うえあいあうううあいああいううう」
という文字列(実際には「あ」や「い」は任意の長さのビット列)であったとします。
この文字を出現回数の昇順に並べると、
う(7回)>あ(5回)>い(2回)>え(1回)
になります。
出現回数の大きいビット列に、短いビット列の符号を対応させるのですが、復元ができる(これを一意復号可能性といいます)ための工夫(注)をして、結果として、
う=0、 あ=10、 い=110、 え=111
の符号を割り当てます。その結果、圧縮後のデータは
01111011010000101101010110000
となり、25ビット(4バイト、全角2文字以下)になります。
○注:符号対応の方法と復元の方法に関しては後述します。 - 符号化の手順
- 符号化の手順は、おおよそ次の通りです。
- 元データを、発生回数の大きい順に並べる。
- 左右の個数がほぼ等しくなる点で二分割し、左側の符号に0、右側の符号を1を追加する。
- 2で分割した部分についても同様にする。
ううううううう あああああ いいい え
< 0 >|< 1 >
|< 0 >|< 1 >
|<0>|<1>
この結果、次のように符号化されます。
う=0、 あ=10、 い=110、 え=111
そして、圧縮後のデータは
01111011010000101101010110000
となります。 - 復元の手順
- 圧縮後のデータと、符号化した対応表を比較していきます。 ・先頭の「0・・・」→先頭が0→う ・次の「111110・・・」→先頭に1が3つ並んでいるので→え ・次の「110110・・・」→先頭の「110」→あ : となり、元のデータが復元できます。 このように復元できるのは「ある記号に対する符号の末尾の何ビットかを除いたビット列が、別の符号と一致してはならない」という条件を満足しているからです。この条件のことを「語頭条件」といい、これを満足する符号のことを「接頭符号」といいます。
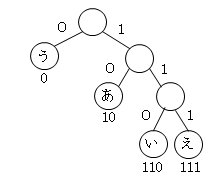
- 符号の木
- ハフマン符号を木構造(2分木)で表現することができます。
この2分木は、次の構造になっています。
節には符号を持たず、葉に元データのビット列がつきます。
0であれば左、1であれば右に枝をだします。
符号は、その葉までに経由した枝の符号をつないだものです。
- LZW
- 辞書圧縮という手法に基づく圧縮方式。辞書圧縮とは、あるデータを圧縮する際、既に読込まれたデータの中からもっとも長い一致文字列を探し、(もし発見できた場合に)その位置と一致長で置き換える方法です。
可逆圧縮で、画像ファイルのGIF形式やTIFF形式の圧縮方式として使われています。
画像等の圧縮
JPEG、PNG、MPEGなどは、ファイル形式であるとともにそれぞれの圧縮方式でもあります。独自の方式やLZWなどの汎用方式に独自の方法を加えたものもあります。
圧縮・解凍ソフトウェア
圧縮は、次の機能をもっています。
・一つあるいは複数のファイルを一つのファイルとして扱うことができる
・そのファイルサイズを小さくすることができる
これにより生成されたファイルをアーカイブ(書庫)といいます。
解凍は、圧縮ファイルを元の形式のファイル群に戻すことです。
しかし、もし元のファイルが同じパソコンにあっても、それを置き換えることではありません。利用者が指定したディレクトリ(解凍場所)に展開されます。
圧縮、解凍は専用のアプリケーションソフトを用います。解凍は同じソフトで圧縮したファイルだけに使えます。代表的な圧縮・解凍ソフトにZIPやLZHなどがあります。OSが標準的に圧縮・解凍ソフトを搭載しています。Windows10 の標準はZIPです。拡張子は zip になります。
他のソフトはフリーソフトとしてダウンロードできます。
また、いくつもの圧縮・解凍ソフトを集めたソフトウェアもあります。
ダウンロードした圧縮ファイルの解凍ソフトをもっていないことを配慮して、圧縮ファイルに解凍用ソフトを加えて一つの圧縮ファイルにすることがあります。ダブルクリックすると解凍できます。それを自己解凍書庫といいます。通常は拡張子が exe になっています。
解凍しようとすると「DLLがありません」というメッセージがでることがあります。DLL(Dynamic Linl Liblary)とは、ソフトウェアを動かすときに合体させる部品ファイルのことです。圧縮、解凍に限定したものではありませんが、多くの圧縮・解凍ソフトはDLLを必要とします。通常は該当ソフトと同梱され同じディレクトリに入っていますが、何らかのトラブルで読めなくなることがあります。これも該当ソフトからダウンロードできます。