スタートページ> JavaScript> 他言語> Python 目次> ←相関・回帰直線・信頼区間・重相関 →判別分析
キーワード:主成分分析、行列式の値、逆行列、固有値、固有ベクトル、連立方程式
np.corrcoef(m), df.corr(), np.linalg.eig, scikit-learn(,sklearn, FactorAnalysis, fa.components_, fa.fit_transform
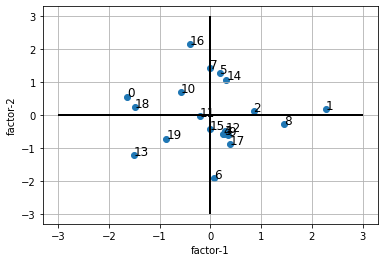
下記の青線の部分をGoogle Colaboratryの「コード」部分にコピーアンドペースト(ペーストは Cntl+V)して実行すれば、右図の画像が表示されます。
主成分分析は次の手順で行います。 ・ 相関行列の計算 np.corrcoef(m), df.corr() ・ 固有値、固有ベクトルの計算 np.linalg.eig(相関行列) ・ 主成分分析 scikit-learn(sklearn)FactorAnalysis FA 因子負荷量の計算 fa.components_ df 各行の主成分値の計算 fa.fit_transform ・ 結果の散布図作成

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.decomposition import FactorAnalysis as FA
# ============================= 入力データ
df = pd.DataFrame([
[3, 4, 4, 5, 4, 4],
[6, 6, 7, 8, 7, 7],
[6, 5, 7, 5, 5, 6],
[6, 7, 5, 4, 6, 5],
[5, 7, 6, 5, 5, 5],
[4, 5, 5, 5, 6, 6],
[6, 6, 7, 6, 4, 4],
[5, 5, 4, 5, 5, 6],
[6, 6, 6, 7, 7, 6],
[6, 5, 6, 6, 5, 5],
[5, 4, 4, 5, 5, 5],
[5, 5, 6, 5, 4, 5],
[6, 6, 5, 5, 6, 5],
[5, 5, 4, 4, 5, 3],
[5, 6, 4, 5, 6, 6],
[6, 6, 6, 4, 4, 5],
[4, 4, 3, 6, 5, 6],
[6, 6, 7, 4, 5, 5],
[5, 3, 4, 3, 5, 4],
[4, 6, 6, 3, 5, 4]],
columns = ['c0','c1','c2','c3','c4','c5'])
# ============= 平均、標準偏差
print('平均\n', df.mean())
print('標準偏差\n', df.std())
# ============= 相関行列
corr = df.corr()
print('相関行列 corr = df.corr()\n',corr)
# ============= 固有値
eig, eigv = np.linalg.eig(corr)
print('固有値 eig = np.linalg.eig(corr)[0]\n',eig)
print('固有ベクトル eigv = np.linalg.eig(corr)[1]\n',eigv)
eign = len(eig[np.where(eig > 1)]) # 1より大の固有値の個数 2
# ============= 主成分分析
fa = FA(n_components=eign, max_iter=500) # 計算方法の指定
fa.fit(df) # この計算方法を df に適用
print('因子負荷量\n', fa.components_) # 主成分での各列の重み付け
print('因子負荷量\n', fa.components_) # 主成分での各列の重み付け
df['f1'] = fa.fit_transform(df)[:,0] # その結果の主成分の値をdfに入れる
df['f2'] = fa.fit_transform(df)[:,1]
print('各点に第1因子、第2因子を付加\n', df)
# ============= グラフの表示
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.scatter(df.f1, df.f2) # 散布図
for i, txt in enumerate(df.index): # 各点の名称表示
ax.annotate(txt, (df.f1[i], df.f2[i]), size=12) # 点の右上に表示されます。
ax.grid()
ax.hlines(y=0, xmin=-3, xmax=3, linewidth=2) # 第1主成分軸を太線で
ax.vlines(x=0, ymin=-3, ymax=3, linewidth=2) # 第2主成分軸
ax.set_xlabel('factor-1')
ax.set_ylabel('factor-2')
fig.show()
平均 c0 5.20 c1 5.35 c2 5.30 c3 5.00 c4 5.20 c5 5.10 標準偏差 c0 0.894 c1 1.039 c2 1.260 c3 1.213 c4 0.894 c5 0.967 相関行列 corr = df.corr() c0 c1 c2 c3 c4 c5 c0 1. 0.486 0.597 0.242 0.276 0.218 c1 0.486 1. 0.557 0.125 0.315 0.172 c2 0.597 0.557 1. 0.240 0.037 0.146 c3 0.242 0.125 0.240 1. 0.436 0.627 c4 0.276 0.316 0.037 0.436 1. 0.583 c5 0.218 0.172 0.146 0.627 0.583 1. 固有値 eig = np.linalg.eig(corr)[0] [2.691 1.521 0.714 0.482 0.256 0.334] 固有ベクトル eigv = np.linalg.eig(corr)[1] [[ 0.430 0.353 -0.056 0.766 0.315 -0.004] [ 0.400 0.384 0.466 -0.538 0.411 -0.122] [ 0.387 0.487 -0.377 -0.210 -0.629 0.172] [ 0.406 -0.377 -0.526 -0.163 0.162 -0.601] [ 0.403 -0.371 0.591 0.199 -0.516 -0.205] [ 0.420 -0.456 -0.098 -0.111 0.204 0.742]] 因子負荷量 [[ 0.514 0.527 0.690 0.766 0.515 0.694] [-0.377 -0.431 -0.752 0.337 0.279 0.433]] 各点に第1因子、第2因子を付加 入力データ 第1因子 第2因子 c0 c1 c2 c3 c4 c5 f1 f2 0 3 4 4 5 4 4 -1.637 0.563 1 6 6 7 8 7 7 2.275 0.184 2 6 5 7 5 5 6 0.851 0.111 3 6 7 5 4 6 5 0.270 -0.574 4 5 7 6 5 5 5 0.249 -0.567 5 4 5 5 5 6 6 0.181 1.277 6 6 6 7 6 4 4 0.069 -1.923 7 5 5 4 5 5 6 0.001 1.420 8 6 6 6 7 7 6 1.455 -0.285 9 6 5 6 6 5 5 0.349 -0.605 10 5 4 4 5 5 5 -0.583 0.702 11 5 5 6 5 4 5 -0.202 -0.021 12 6 6 5 5 6 5 0.294 -0.494 13 5 5 4 4 5 3 -1.503 -1.222 14 5 6 4 5 6 6 0.317 1.079 15 6 6 6 4 4 5 -0.013 -0.424 16 4 4 3 6 5 6 -0.400 2.152 17 6 6 7 4 5 5 0.379 -0.890 18 5 3 4 3 5 4 -1.487 0.231 19 4 6 6 3 5 4 -0.866 -0.715
このような特定分野では、それに特化した関数やライブラリが提供されています。
分散共分散行列:元のデータから平均を引いて計算する
相関行列:元のデータを平均0標準偏差1に標準化してから計算する
の違いがあります。結果では相関行列のほうが標準偏差だけ小になります
共分散行列
nparray: cov = np.cov(m, options)
options
rowvar=0/1 # 0:横に計算(省略時) 1:縦に計算
bias=0/1 # 0:不偏分散(省略時) 1:標本分散)
DataFrame: cov = df,cov() # 常に縦方向、不偏分散
相関行列
nparray: corr = np.corrcoef(m, options)
options
rowvar=0/1 # 0:横に計算(省略時) 1:縦に計算
bias=0/1 # 0:不偏分散(省略時) 1:標本分散)
DataFrame: corr = df.corr() # 常に縦方向、不偏分散
numpy.linalg は NumPy のサブセットで線形代数の分野で便利な機能を提供します。
import numpy.linalg as LA
で利用可能になります。
LA.xxx() のように記述できますが、np.linalg.xxx() の形式も可能です。xxx は NumPy 自体と同名のものがあり、そのときは np.xxx としても矛盾は生じません。
行列式の値 = np.linalg.det(正方行列) m = [[1, 2], [3, 4]] # list でも ndarray でもよい np.linalg.det(m) # -2. (= 1*4 - 2*3) 逆行列 = np.linalg.inv(正方行列) m = [[1, 2], [3, 4]] np.linalg.inv(m) # array([[-2., 1.], [1.5, -0.5]]) 固有値, 固有ベクトル = np.linalg.eig(正方行列) 統計処理では、この正方行列は通常は相関行列です。 サイズが n*n ならば、固有ベクトルは n*n 、固有値は n の ndarrayに配列になります m = [[4, 1], [6, 5]] 固有値, 固有ベクトル = np.linalg.eig(m) # 左辺は2変数になります 固有値 # array([2., 7.]) 固有ベクトル # array([[-0.447, -0.316], # [ 0.894, -0.948]]) # ↑ ↑ # 固有値=2 =7 のときの固有ベクトル 連立方程式の解 = np.linalg.solve(係数行列, 定数項) a = [[1, 2], [3, 4]] # 1X+2Y= 5 b = [5, 11] # 3X+4Y=11 np.linalg.solve(a, b) # array([1., 2.])
scikit-learnは、データ分析やデータマイニングに使われる機械学習ライブラリです。次元縮小関連クラスのsklearn.decompositionサブモジュールがあり、回帰分析や主成分分析などに広く用いられています。
from sklearn.decomposition import FactorAnalysis as FA
として使用用可能にします。
主成分分析は、np.linalg.eig で固有値、固有ベクトルを算出した後、次のステップで行います fa = FA(n_components=主成分数) # 主成分のモデルを生成 fa.fit(x) # 配列 x をモデルに適合させる fa.components_ # 因子負荷量 各列での重み付け。下表 第1主成分 [[ 0.514 0.527 0.690 0.766 0.515 0.694] 第2主成分 [-0.377 -0.431 -0.752 0.337 0.279 0.433]]
あるデータの主成分を求めるには、この値とCの積和を計算すればよいのですが、(C-平均)/標準偏差 の正規化を行っていますので、その変換をした値 s を用いる必要があります。~などと試行錯誤したのですが、Cとfとの関係式がわからないままです。ご指導いただければ幸甚です。