スタートページ＞ JavaScript＞ ライブラリ目次

行列関連 JavaScript関数ライブラリ mtx.js の利用解説書

ご利用にあたって

行列（２次元配列）の基本的な操作を掲げます。

mtxDet　行列式の値
　　mtxDetTrace(表示場所, 正方行列)　コード表示
　　var 値 = mtxDet(正方行列)　コード表示

正方行列式の値（determinant）を求めます。
　　３次までは、サラスの式により直接計算します。
　　４次以上は、余因子展開で低次にし、再帰により３次にして計算します。

ここでは、行列・余因子のピボットになる列を０に固定しています。
しかし、ピボットが０になるように
、 　　ピボット列を設定したり
　　行列式や余因子行列式を変形すると
計算量が少なくできます（その操作により大になることもありますが）
それには、次の性質が便利です。
　　独立ではない行、あるいは列があると、値は０になる。
　　ある列を定数倍して他の列に加えても行列式の値は変わらない。
　　三角行列式の値は対角要素の積になる。 　　列や行を入れ替えると積の正負が逆転する

ケース１　３次　サラスの式により直接計算

　　var 正方行列 　　　　　= [[ 3, 4, -1],
　　　　　　 [ 2, 5, -2],
　　　　　　 [ 1, 6, -4] ];
var 値 = mtxDet(正方行列);
Trace Return

ケース２　４次　余因子展開

　　var 正方行列
　　　　　 = [[ 2, 1, 5, 3],
　　　　　　　[ 3, 0, 1, 6],
　　　　　　　[ 1, 4, 3, 3],
　　　　　　　[ 8, 2, 0, 1] ];
　　var 値 = mtxDet(a);

ケース３

mtxVandermondeDet ヴァンデルモンド行列式の式の値
　　mtxVandermondeDetTrace(表示場所, 正方行列); 　コード表示
　　var 値 = mtxVandermondeDet(正方行列); 　コード表示

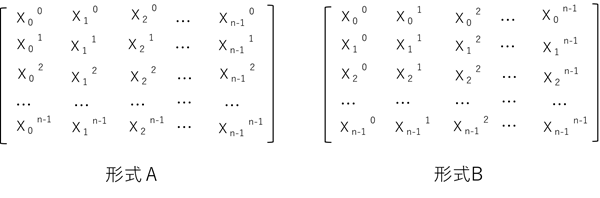
ヴァンデルモンド行列式とは、下図の形式Ａのように、ｉ行の要素がx_jのi乗である正方行列のことです。先頭行は各列の要素がｘ⁰＝１になります。また、形式Ｂのように、先頭列を１とする行列もヴァンデルモンド行列式といいます。
ここでは、形式Ａを対象にしますが、形式Ｂでも同じ結果になります。

ヴァンデルモンド行列式は、x_jを与えれば自動的に生成できるので、ここでは一次元配列で与えることにします。また、x₀ < x₁ < x₂ < … < x_n-1 のように同一値をもたず昇順になっているものとします。

ケース１

ケース２

mtxVandermondeEq ヴァンデルモンド行列による高次元連立方程式の係数決定
　　mtxVandermondeEqTrace(表示場所, 正方行列); 　コード表示
　　var 係数 = mtxVandermondeEq(正方行列); 　コード表示

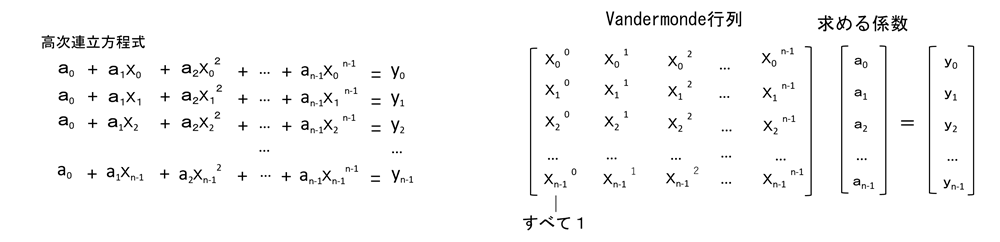
下右図のような n 個の説明変数 x と被説明変数 y による n-1 次の連立方程式の、係数 a を算出します。
これは、n 個の点 (x_i, x_i) を通る曲線の式を求めることになります。
この高次連立方程式を行列で表示すると下右図になります。その正方行列をヴァンデルモンド行列といいます。

係数 a[k] = 分子 / 分母
　　分母：元のヴァンデルモンド行列の値
　　分子：分母の k 列を y_i で置き換えた行列の値
　　　　この計算にもヴァンデルモンド行列の計算方法が利用できるのではないかと思いますが、
　　　　私は理解していないので、通常の行列氏の値を計算する方法を用いています。
　　　　（外部関数mtxDetを呼び出しています）

ケース１

ケース２

mtxInv 逆行列
　　mtxInvTrace(表示場所, 正方行列)　コード表示
　　var 逆行列 = mtxInv(正方行列)　コード表示

行・列のサイズn の正方行列 a[i][j] の逆行列を、ガウス=ジョルダンの掃出法で求めます。

ケース１

ケース２

mtxInvEq 逆行列と連立方程式の解
　　mtxInvEqTrace(表示場所, 行列)　コード表示
　　var 逆行列 = mtxInvEq(行列)　コード表示

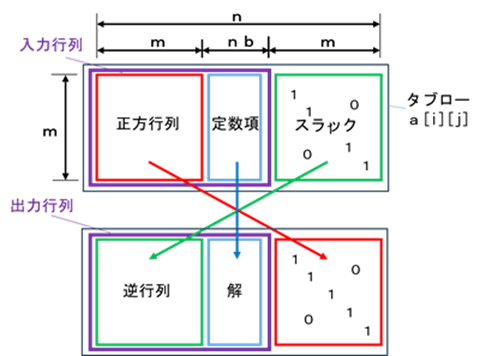
右図で正方行列を入力すると、逆行列が得られます。
正方行列を係数とし、定数項を入力にすると、連立方程式になり、逆行列と解が出力されます。
計算方法はガウス=ジョルダンの掃出法を用います。

ケース１　逆行列のみ

ケース２　逆行列と連立方程式

ケース３

mtxInvS　対称行列の逆行列
　　rtn = mtxInvS(対称行列)　コード表示

共分散行列や相関行列のように、対角要素が０でない対称行列の逆行列を求めます。
対角要素を順に pivot とすればよいので単純になります。

ケース１

    var 対称行列
            = [ [42.00, 15.00, 24.50],
              [15.00, 31.50, 21.25],
              [24.50, 21.25, 35.88] ];

ケース２

対称行列なので右上半分だけでよい。

mtxLuDoolittle ＬＵ分解(Doolittle法)
　　mtxLuDoolittleTrace(表示場所, 正方行列); 　コード表示
　　var [下三角行列, 上三角行列] = mtxLuDoolittle(正方行列); 　コード表示

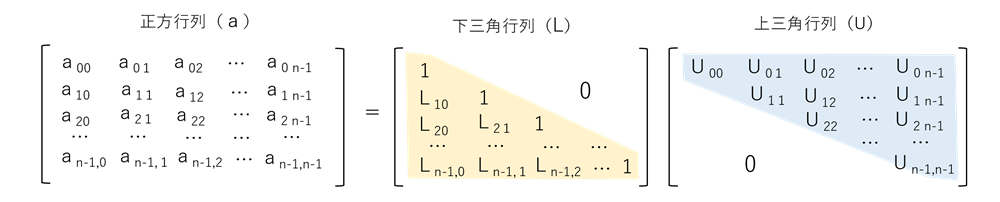
ＬＵ分解とは、下図のように、正方行列（ａ）を下三角行列（L)と上三角行列（Ｕ）の積に分解することです。Ｌの対角要素は１になります。
その代表的な解法にDoolittle法とGause法がありますが、ここではDoolittle法を用います。
Doolittle法は計算負荷が小さいのですが、ここでは次の制約を設けました。
　　正方行列のサイズを４以下とします。
　　計算経過で対角要素が０になると打ち切ります。

ケース１　サイズ＝２のとき

　　┌１　２┐＝┌１　０┐　┌１　２┐
　　└３　４┘　└３　１┘　└０　-2┘
入力
　var 正方行列 = [ [1, 2], [3, 4] ];
　var [下三角行列, 上三角行列] = mtxLuDoolittle(正方行列);
Trace Return

ケース２　サイズ＝３のとき

　　┌２　３　-1┐　┌１　０　０┐　┌２　３　-1┐
　　│４　４　-3│＝│２　１　０│　│０　-2　-1│
　　└-2　３　-1┘　└-1　-3　１┘　└０　０　-5┘
入力
　var 正方行列 = [ [2, 3, -1], [4, 4, -3], [-2, 3, -1 ] ];
　var [下三角行列, 上三角行列] = mtxLuDoolittle(正方行列);
Trace Return

ケース３　サイズ＝４のとき

　　┌１　２　１　２┐　┌１　０　０　０┐　┌１　２　１　２┐
　　│１　３　３　３│＝│１　１　０　０│　│０　１　２　１│
　　│２　５　６　７│　│２　１　１　０│　│０　０　２　２│
　　└２　４　４　７┘　└２　０　１　１┘　└０　０　０　１┘
入力
　var 正方行列 = [ [1, 2, 1, 2], [1, 3, 3, 3], [2, 5, 6, 7], [2, 4, 4, 7] ];
　var [下三角行列, 上三角行列] = mtxLuDoolittle(正方行列);
Trace Return

ケース４

mtxLuGauss ＬＵ分解（Gauss法）
　　mtxLuGaussTrace(表示場所, 正方行列); 　コード表示
　　var [置換後正方行列, 下三角行列, 上三角行列] = mtxLuGauss(正方行列); 　コード表示

ＬＵ分解とは、下図のように、正方行列（ａ）を下三角行列（L)と上三角行列（Ｕ）の積に分解することです。ｌの対角要素は１になります。
その代表的な解法にDoolittle法とGause法（掃出法）がありますが、ここではGause法を用います。
場合によっては掃出処理中にピボットが０になることがあります。そのときは下行のピボット列が非０の行と置換します。
そのため、の行も置換されます（呼出側の正方行列は変化しません）。置換後の行列は、置換後正方行列として戻されます。

ケース１　サイズ＝３のとき

　　┌２　３　-1┐　┌１　０　０┐　┌２　３　-1┐
　　│４　４　-3│＝│２　１　０│　│０　-2　-1│
　　└-2　３　-1┘　└-1　-3　１┘　└０　０　-5┘
入力
　var 正方行列 = [ [2, 3, -1], [4, 4, -3], [-2, 3, -1 ] ];
　var [置換後正方行列, 下三角行列, 上三角行列] = mtxLuGauss(正方行列);
Trace Return

ケース２　置換なし

　　┌１　２　１　２┐　┌１　０　０　０┐　┌１　２　１　２┐
　　│１　３　３　３│＝│１　１　０　０│　│０　１　２　１│
　　│２　５　６　７│　│２　１　１　０│　│０　０　２　２│
　　└２　４　４　７┘　└２　０　１　１┘　└０　０　０　１┘
入力
　var 正方行列 = [ [1, 2, 1, 2], [1, 3, 3, 3], [2, 5, 6, 7], [2, 4, 4, 7] ];
　var [置換後正方行列,下三角行列, 上三角行列] = mtxLuGauss(正方行列);
Trace Return

ケース３　置換あり

　　┌１　２　１　２┐　┌１　０　０　０┐　┌１　２　１　２┐
　　│２　４　４　７│＝│１　１　０　０│　│０　１　２　１│
　　│２　５　６　７│　│２　１　１　０│　│０　０　２　２│
　　└１　３　３　３┘　└２　０　１　１┘　└０　０　０　１┘
入力
　var 正方行列 = [ [1, 2, 1, 2], [2, 4, 4, 7], [2, 5, 6, 7], [1, 3, 3, 3] ];
　var [置換後正方行列,下三角行列, 上三角行列] = mtxLuGauss(正方行列);
Trace Return

ケース４

mtxQr ＱＲ分解(グラム・シュミット法)
　　mtxQrTrace(表示場所, A); 　コード表示
　　var [Q, R] = mtxQr(A); 　コード表示

ＱＲ分解とは、下図のように、m×n の行列Ａを m×m の直交行列Ｑと m×n の上三角行列Ｒ の積に分解することです。
（ここでは m=n すなわち「Ａは正方行列」に限定します。）
　最も単純な解法であるグラム・シュミット法を用います。
　　直交行列：それぞれの列、行が互いに直交した単位ベクトルである行列
　　上三角行列：右下の要素がすべて０である行列
直交行列式の値は±１、三角行列式の値は対角要素の積なので、Ａの行列式の値は（±対角要素の積）になります。

ケース１　３x３のとき

　　┌ 1　1 -1 ┐＝┌ 0.58　0.15 -0.80 ┐ ┌ 1.73 1.15 1.73 ┐
　　│ 1 -1　1 │　│ 0.58 -0.77　0.27 │ │ 0　　2.16 0.93 │
　　└ 1　2　3 ┘　└ 0.58　0.62 0.53 ┘ └ 0　　0　　2.67 ┘
入力
　　var a = [ [1, 1, -1], [1, -1, 1], [1, 2, 3] ];
　　var [q, r] = mtxQr(a);
出力
　　q = 0.58　0.15 -0.80　　　r = 1.73 1.15 1.73
　　　　0.58 -0.77　0.27　　　　　0　　2.16 0.93
　　　　0.58　0.62　0.53　　　　　0　　0　　2.67
Trace Return

ケース２

mtxSimAlt 正方行列→対称行列＋交代行列
　　var [対称行列, 交代行列」 = mtxSimAlt(正方行列);　コード表示

例示すれば、次のような分割操作です。
　　┌　１－１　０┐　┌　１　０－２┐　┌　０－１　２┐
　　│　１　３－４│＝│　０　３－１│＋│　１　０－３│
　　└ー４　２　４┘　└－２－１　４┘　└－２　３　０┘
　　　　正方行列　　＝　　対称行列　　＋　　交代行列
　　　　　Ａ　　　　　（Ａ＋Ａ^Ｔ）／２　（Ａ－Ａ^Ｔ）／２
　　（Ａ^ＴはＡの転置行列）
　　　　┌　１　１－４┐
　　　　│－１　３　２│
　　　　└　０－４　４┘

ケース１（上の例）

ケース２

mtxDiagReg 正方行列→正則行列、対角行列　2x2 3x3 に限定
　　mtxDiagRegTrace(表示場所, 正方行列);　コード表示
　　var [固有値, 固有ベクトル, 正則行列, 対角行列]
　　　　　 = mtxDiagReg(正方行列);　コード表示

対角行列（Ｄ）＝正則行列（Ｐ）^-1・正方行列（Ａ）・正則行列（Ｐ）
となる正則行列と対角行列を求めます。
　対角行列（Diagonai Matrix）：非対角要素がすべて０である行列
　正則行列（Regular Matrix：逆行列が存在する行列。

　正方行列(Ａ)
　 　┌３　１┐
　 　└２　２┘
　固有値（λ=1,4）固有ベクトルを計算して、固有ベクトルの転置行列が正則行列になります、
　 　　　正則行列(Ｐ)　　逆行列(Ｐ^-1)
　　　　┌　１　１┐ 　┌１/3－２/3┐
　　　　└ー２　１┘ 　└２/3　１/3┘
　対角行列（Ｄ）は　Ｐ^-1ＡＰ　により求められます。
　　　　┌１/3－２/3┐ｘ┌３　１┐ｘ┌　１　１┐＝┌１　０┐
　　　　└２/3　１/3┘　└２　２┘　└ー２　１┘　└０　４┘

ケース１（上の例）

ケース２

mtxKaidan 行列→階段行列、ランク
　　mtxKaidanTrace(行列);　コード表示
　　var [階段行列, ランク] = mtxKaidan(行列); 　コード表示

階段行列とは、上三角行列の特殊な形式です。下図のように、上三角行列は対角成分より下の成分が０ならばよいのですが、階段行列では「各行各行の主成分（０でない成分。赤の成分）が下の行の主成分よりも左側にある」条件が加えられます。
下左図の上三角行列では⑥が⑤の右側になるので、階段行列ではありません。
下右図で、主成分から右の部分を矩形で囲むと、階段状になります。それで階段行列といいます。

階段行哲は、次の用途に使われています。
　　行列のランクの取得　　ここで扱います。
　　連立方程式の求解（解なし、不定解も含む）　mtxKaidanEq で扱います。

ここでの制約：
　　階段行列の対角成分が、ランク行では非零、それ以外は１になる場合だけを対象にします。
　　図の３列のように、対角成分が０になるような場合は対象にしていません。
　　そのため、実際には階段行列が存在するのに、ここではエラーになる場合があります。

ケース１　ｍ(行数)＝ｎ(列数)　（正方行列）正則行列（全行が独立ベクトル）

ケース２　ｍ＝ｎ（正方行列）正則行列（非独立ベクトルあり）

ケース３　ｍ＞ｎ（縦長行列）

ケース４　ｍ＜ｎ（横長行列）

ケース５　非零のピボットが存在しないとき

ケース６

mtxKaidanEq 階段行列を用いた連立方程式の解
　　mtxKaidanEqTrace(表示場所, 行列);　コード表示
　　var x = mtxKaidanEq(行列); 　コード表示

階段行列および行列のランクを計算するには、外部変数 mtxKaidan を用いています、
それに合わせるため、入力行列の左側を係数表とし定数項を末尾列に追加します。
ここでは行列のサイズを次の記号で示します。
　　ｎｘ：変数の個数
　　ｎ（nx+1）：定数項を含む行列の列数
　　ｍ：行列の行数
　　ランク：非独立の行を除いた行数。階段行列に変形したときの段数
一次連立方程式の解は次の３形態に分かれます。
　　確定解：ランク＝ｎｘのときは、唯一の確定した解が得られます。
　　不定解：ランク＜ｎｘのときは、確定解に一部変数をパラメタとする式が解になります。
　　解なし：ランク＞ｎｘのときは、方程式間で矛盾があり、解が存在しません。
mtxKaidanEqの特徴は、これらのどの形態にも対応できることにあります。

ケース１

ケース２

mtxEigen　固有値
　　mtxEigenTrace(表示場所, 正方行列)　コード表示
　　var λ = mtxEigen(正方行列)　コード表示

かなり高度・複雑な処理なので、次の制約を設けました。
　・次数は２次あるいは３次だけとする。
　・固有値は実固有値だけを対象にする。

（注）多変量解析では、高次の対称行列から、実数で絶対値の大きい固定値を２，３個だけ必要なことがあります。 その目的には、maEigenPowerがあります。

ケース１（2*2）

ケース２（3*3）

ケース３

mtxEigenVector 固有ベクトル
　　mtxEigenVectorTrace(表示場所, 正方行列) 　コード表示
　　var [λ, 固有ベクトル] = mtxEigenVector(正方行列) 　コード表示

かなり高度・複雑な処理なので、次の制約を設けました。
　・次数は２次あるいは３次だけとします。
　：固有値がすべて異なる実数値のときだけ固有ベクトルを計算します。

（注）多変量解析では、高次の対称行列から、実数で絶対値の大きい固定値を２，３個だけ必要なことがあります。 その目的には、maEigenPowerがあります。

ケース１（２＊２）

入力
　　var 正方行列 = [ [ 3, 1,], [2, 2] ];
　　var λ = mtxEigen(正方行列);
出力
　　λ[0]=1; V[0][0]=-0.5; V[0][1]=1
　　λ[1]=4: V[1][0]= 1;　 V[1][1]=1
Trace実行 Return実行

ケース２（３＊３）

ケース３

mtxMul　行列の積
　　mtxMultrace(表示場所, 行列Ａ, 行列Ｂ)　コード表示
　　var 行列Ｃ = mtxMul(行列Ａ, 行列Ｂ)　コード表示

mxn の行列Ａとnxp の行列Ｂの積 mxp の行列Ｃを計算します。

ケース１

ケース２

mtxPow　正方行列の累乗
　　mtxPowTrace(表示場所, 正方行列,乗)　コード表示
　　var 累乗行列 = mtxPow(正方行列,乗)　コード表示

累乗行列 = 正方行列^乗 の計算をします。
本来ならばＱＲ分解を用いるべきですが、ここでは単純に行列の積を繰り返しています。

ケース１

ケース２

行列のソート（行を変える）
　　mtxSort(行列, {fix=xx, key1=xx, ad1=xx, key2=xx. ad2=xx} )　コード表示

最大２個のソートキー列で行列をソートする
 　　行列：ソートする行列　元の行列は保持されない
 　　fix：ソートしない先頭行数（行番号ではない）たとえば先頭行１行が列名ならば fix=1
 　　key1：優先順位１のソートキー行番号　必須
 　　ad1：指定しなければkey1での昇順、指定すれば（"disc" でも -1 でもよい）降順
 　　key2：優先順位２のソートキー行番号　オプション
 　　ad1：指定しなければkey1での昇順、指定すれば（"disc" でも -1 でもよい）降順
入力した行列は保存されずソート後の状態になります。

ケース１

    var 行列 = [ [ 1,  10,  "A"],
              [ 3,  10,  "B"],
              [ 2,  10,  "C"],
              [ 2,  20,  "D"],
              [ 1,  20,  "E"],
              [ 2,  20,  "F"] ];
    mtxSort(行列, { key1:0 });

ケース２

a はケース１と同じ
列０の昇順、列１の降順にソート
    mtxSort(行列, { key1:0, key2:, ad2:"desc" });

ケース３

    var 行列 = [ ["x", "Y", "Z"],  // 固定行　fix=1
              [ 1,  10,  "A"],
              [ 3,  10,  "B"],
              [ 2,  20,  "C"],
              [ 2,  10,  "D"],
              [ 1,  20,  "E"],
              [ 2,  20,  "F"] ];
                    └　この列の昇順にソート
    mtxSort(行列, { key1:1 });

行列の順序付け
　　順位 = mtxOrder(行列, {fix=xx, key1=xx, ad1=xx, key2=xx. ad2=xx} )　コード表示

行列ａについて、指定列key1, key2の値により昇順または降順にソートしたときの各行の順位を戻します。行列そのものはソートされません。
順位[k] = i とは、ソートしたとき、k番目になる行が i であることを示します。
すなわち、行列[[順位[k]][j] がｋ番目の行になります。

 　　行列：ソートする行列　元の行列は保持されない
 　　fix：ソートしない先頭行数（行番号ではない）たとえば先頭行１行が列名ならば fix=1
 　　key1：優先順位１のソートキー行番号　必須
 　　ad1：指定しなければkey1での昇順、指定すれば（"disc" でも -1 でもよい）降順
 　　key2：優先順位２のソートキー行番号　オプション
 　　ad1：指定しなければkey1での昇順、指定すれば（"disc" でも -1 でもよい）降順

ケース１

    var 行列 = [ [ 1,  10,  "A"], // 順位[1]    順位[0] = 4  [ 1,  20,  "E"]
              [ 3,  10,  "B"],    // 順位[5]    順位[1] = 0  [ 1,  10,  "A"]
              [ 2,  20,  "C"],    // 順位[2]    順位[2] = 2  [ 2,  20,  "C"]
              [ 2,  10,  "D"],    // 順位[4]    順位[3] = 5  [ 2,  20,  "F"]
              [ 1,  20,  "E"],    // 順位[0]    順位[4] = 3  [ 2,  10,  "D"]
              [ 2,  20,  "F"] ];  // 順位[3]    順位[5] = 1  [ 3,  10,  "B"]
    var 順位 = mtxOrder(行列, { key1:0, key2:1, ad2:"desc" });
    // mtxSort のケース２と同じ指定

多変量解析でのデータ入力形式について

多変量解析での入力データは、データフレーム形式にするのが通常です。
それに対して、実務でのデータでは、表計算スプレッドシートやリレーショナルデータベースのように
　　Df = [ [ 行名　　特性ｙ　特性x1　特性x2 ],
　　　     [ 標本Ａ,　200,     10,     50 ],
　　　     [ 標本Ｂ,  101,     31,     61 ],　　形式１
　　　     [ 標本Ｃ,　402,     22,     82 ],
　　　     [ 標本Ｄ,  303,     43,     73 ] ];
  あるいは  
        Df  = [[ 200,  10,  50 ],
               [ 101,  31,  61 ],　　　　　　　 形式２
               [ 402,  22,  82 ],
               [ 303,  43,  73 ] ];
         colname = [ 特性ｙ,　特性x1,　特性x2 ];
         rowname = [ 標本Ａ,  標本Ｂ,　標本Ｃ, 標本Ｄ ];
　行名、列名が不要なときは
        Df  = [[ 200,  10,  50 ],
               [ 101,  31,  61 ],　　　　　 　　形式３
               [ 402,  22,  82 ],
               [ 303,  43,  73 ] ];
  のように、標本をレコードとして（行側にして）特性を属性（列側にして）与えるのが自然ですし管理も容易です。

ところが、多くの統計処理のプログラムでは（ここでの関数もそうですが）、
               標本Ａ 標本Ｂ　標本Ｃ 標本Ｄ
    特性 y  =  [ 200,   101,    402,   303 ];
    特性 x1 =  [  10,    31,     22,    43 ];　　形式４
    特性 x2 =  [  50,    61,     82,    73 ];
  あるいは 
         x  = [[ 200,   101,    402,   303 ],
               [  10,    31,     22,    43 ],　　形式５
               [  50,    61,     82,    73 ] ];
  のように、特性値を主として（行側にして）与えるのが通常です。

そのため、データフレーム形式１～３の転置行列を生成することになります。ここでは形式５を生成することにします。
簡単な処理なので、あえて関数にする必要はないでしょうが・・・。

単に Df の転置行列 x を作るだけ
    var Df  = [[ 200,  10,  50 ],
               [ 101,  31,  61 ],
               [ 402,  22,  82 ],
               [ 303,  43,  73 ] ];

　　行名は存在しない。あるいは、行名も xT に入れる
    var Df = [ ["特性ｙ","特性x1","特性x2" ],
               [  200,     10,      50 ],
               [  201,     31,      61 ],
               [  402,     22,      82 ],
               [  303,     43,      73 ] ];

　　行名が存在し、取り出して rowname に入れる
    var Df = [ [ "行名", "特性ｙ", "特性x1", "特性x2" ],
               [ "標本Ａ",  200,     10,     50 ],
               [ "標本Ｂ",  101,     31,     61 ],
               [ "標本Ｃ",  402,     22,     82 ],
               [ "標本Ｄ",  303,     43,     73 ] ];